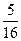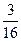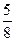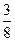题目内容
在一个盒子中有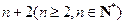
个球，其中2个球的标号是不同的偶数，其余n个球的标号是不同的奇数。甲乙两人同时从盒子中各取出2个球，若这4个球的标号之和为奇数，则甲胜；若这4个球的标号之和为偶数，则乙胜。规定：胜者得2分，负者得0分。
（I）当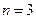
时，求甲的得分
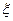的分布列和期望；
（II）当乙胜概率为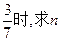
的值
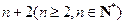个球，其中2个球的标号是不同的偶数，其余n个球的标号是不同的奇数。甲乙两人同时从盒子中各取出2个球，若这4个球的标号之和为奇数，则甲胜；若这4个球的标号之和为偶数，则乙胜。规定：胜者得2分，负者得0分。（I）当
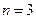时，求甲的得分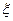的分布列和期望；（II）当乙胜概率为
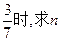的值（I）略
（II）
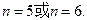
解：（I）当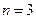时，甲胜的概率为
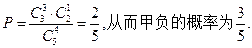…………5分
故甲的得分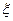的分布列为
…………6分
故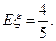
…………7分
（II）当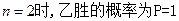
，不合题意；
当n=3时，乙胜的概率为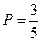
，不合题意 ； …………8分
当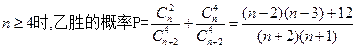
…………11分
故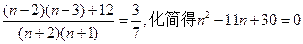
，…………12分
解得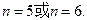 …………14分
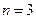时，甲胜的概率为 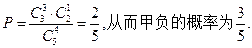…………5分故甲的得分
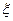的分布列为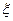 | 2 | 0 |
| P |  |  |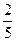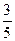
故
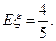…………7分（II）当
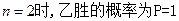，不合题意；当n=3时，乙胜的概率为
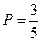，不合题意 ； …………8分当
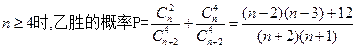
…………11分
故
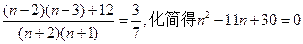，…………12分解得
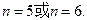…………14分
练习册系列答案
同步练习强化拓展系列答案
相关题目
题构成，每个选择题有4个选项，其中有且仅有一个选项是正确答案，每题选择正确答案得5分，不作出选择或选错不得分，满分100分.学生甲选对任一题的概率为0.9，学生乙则在测验中对每题都从4个选择中随机地选择一个，求学生甲和乙在这次英语单元测验中的成绩的期望 
的分布列与期望.
；②
；③
；④
；
；⑥
的分布列和数学期望。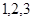
的三个小球.某人做如下游戏：每次从袋中摸一个小球，记下标号然后放回，共摸球
次.若拿出球的标号是奇数,则得
分,否则得
分，则
的分布列如下表，随机变量
，则
的值为（ ）
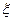表示取出的3个小球上的最大数字，
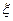服从B（6，
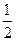），则P（
