题目内容
6.已知函数f(x)为y=3x,x∈[0,2]的反函数,g(x)=[f(x)]2+f(x2),若g(x)≤k恒成立,求实数k的取值范围.(注意反函数f(x)的定义域与g(x)的定义域)分析 根据条件得到f(x)=log3x,x∈[1,9],进而求得g(x)=[f(x)]2+f(x2)=(log3x+1)2-1,再求最大值即可.
解答 解:因为f(x)是y=3x,x∈[0,2]的反函数,
所以,f(x)=log3x,x∈[1,9],
g(x)=[f(x)]2+f(x2)=log32x+2log3x=(log3x+1)2-1,
又∵f(x)的定义域为[1,9],
∴g(x)的自变量需满足$\left\{\begin{array}{l}{1≤x≤9}\\{1≤x^2≤9}\end{array}\right.$,解得x∈[1,3],
因此,log3x∈[0,1],
故g(x)min=g(1)=0,g(x)max=g(3)=3,
要使g(x)≤k恒成立,则k≥g(x)max=3.
所以,实数m的取值范围为[3,+∞).
点评 本题主要考查了反函数和复合函数定义域的解法,二次函数最值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知i虚数单位,则($\frac{1+2i}{1-i}$)2-($\frac{2-i}{1+i}$)2=( )
| A. | -3+4i | B. | 0 | C. | -4+3i | D. | -4-3i |
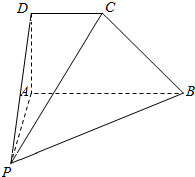 如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1
如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1