题目内容
16.已知向量$\overrightarrow{a}$=($\sqrt{3},\sqrt{5}$),|$\overrightarrow{b}$|=2,求满足下列条件的$\overrightarrow{b}$的坐标.(1)$\overrightarrow{a}$⊥$\overrightarrow{b}$(2)$\overrightarrow{a}$∥$\overrightarrow{b}$.
分析 (1)设出向量$\overrightarrow{b}$的坐标,由|$\overrightarrow{b}$|=2以及$\overrightarrow{a}$⊥$\overrightarrow{b}$,列出方程组求出$\overrightarrow{b}$的坐标;
(2)由|$\overrightarrow{b}$|=2和$\overrightarrow{a}$∥$\overrightarrow{b}$,列出方程组求出$\overrightarrow{b}$的坐标即可.
解答 解:设$\overrightarrow{b}$=(x,y),
∵|$\overrightarrow{b}$|=2,∴x2+y2=4①;
又向量$\overrightarrow{a}$=($\sqrt{3},\sqrt{5}$),
(1)当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,
$\sqrt{3}$x+$\sqrt{5}$y=0②;
由①、②组成方程组,
解得$\left\{\begin{array}{l}{x=-\frac{\sqrt{10}}{2}}\\{y=\frac{\sqrt{6}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{\sqrt{10}}{2}}\\{y=-\frac{\sqrt{6}}{2}}\end{array}\right.$;
∴$\overrightarrow{b}$=(-$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{6}}{2}$)或$\overrightarrow{b}$=($\frac{\sqrt{10}}{2}$,-$\frac{\sqrt{6}}{2}$);
(2)当$\overrightarrow{a}$∥$\overrightarrow{b}$时,
$\sqrt{3}$y-$\sqrt{5}$x=0③;
由①、③组成方程组,
解得$\left\{\begin{array}{l}{x=\frac{\sqrt{6}}{2}}\\{y=\frac{\sqrt{10}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{6}}{2}}\\{y=-\frac{\sqrt{10}}{2}}\end{array}\right.$;
∴$\overrightarrow{b}$=($\frac{\sqrt{6}}{2}$,$\frac{\sqrt{10}}{2}$)或$\overrightarrow{b}$=(-$\frac{\sqrt{6}}{2}$,-$\frac{\sqrt{10}}{2}$).
点评 本题考查了平面向量的模长与平行和垂直的坐标表示问题,也考查了方程组的解法与应用问题,是基础题.

 阅读快车系列答案
阅读快车系列答案| A. | 7 | B. | 7或$\frac{1}{7}$ | C. | -7 | D. | $-\frac{1}{7}或7$ |
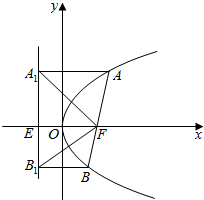 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
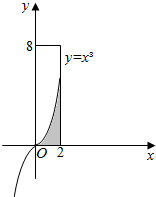 利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.
利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.