题目内容
15.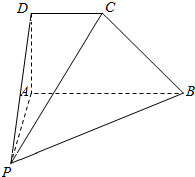 如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1
如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1(1)求证:BC⊥平面PAC;
(2)试在线段PB上找一点M,使CM∥平面PAD,并说明理由;
(3)若点M是由(2)中确定的,且PA⊥AB,求四面体MPAC的体积.
分析 (1)(1)连接AC,过C作CE⊥AB,垂足为E,则四边形ADCE是正方形.△BCE为等腰直角三角形,得出BC⊥AC,已知BC⊥PC,故BC⊥平面PAC;
(2)当M为PB中点时,CM∥平面PAD,取AP中点F,连接CM,FM,DF,可易证四边形CDFM为平行四边形,推出CM∥DF,故CM∥平面PAD.
(3)因为M为PB中点,可得V棱锥M-PAC=$\frac{1}{2}$V棱锥B-PAC,利用勾股定理可解得BC,AC的长度,代入体积公式计算出体积.
解答 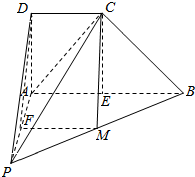 解:(1)连接AC,过C作CE⊥AB,垂足为E,
解:(1)连接AC,过C作CE⊥AB,垂足为E,
∵AD⊥AB,CD∥AB,AD=DC,
∴四边形ADCE是正方形.
∴∠ACD=∠ACE=45°.
又∵AE=CD=$\frac{1}{2}$AB,∴BE=AE=CE.
∴∠BCE=45°.∴∠ACB=90°.∴AC⊥BC.
又∵BC⊥PC,AC∩PC=C,
∴BC⊥平面PAC.
(2)当M为PB中点时,CM∥平面PAD.
证明:取AP中点F,连接CM,FM,DF.
则FM∥AB,且FM=$\frac{1}{2}AB$,∵CD∥AB,CD=$\frac{1}{2}$AB,
∴FM∥CD,FM=CD.
∴四边形CDFM为平行四边形,∴CM∥DF.
∵DF?平面PAD,CM?平面PAD,∴CM∥平面PAD.
(3)由(1)知,BC⊥平面PAC,M为PB中点,
所以点M到平面PAC的距离等于$\frac{1}{2}$BC,V棱锥M-PAC=$\frac{1}{2}$V棱锥B-PAC.
在三角形ABP中,∵PA⊥AB,∴PB=$\sqrt{5}$,∴PC=$\sqrt{3}$,∵AC=$\sqrt{2}$,PA=1,∴△PAC是直角三角形,
S△PAC=$\frac{1}{2}$×$\sqrt{2}$=$\frac{\sqrt{2}}{2}$,
∴V棱锥M-PAC=$\frac{1}{2}$V棱锥B-PAC=$\frac{1}{6}$S△PAC•BC=$\frac{1}{6}$×$\frac{\sqrt{2}}{2}$×$\sqrt{2}$=$\frac{1}{6}$.
点评 本题考查了线面垂直,线面平行的判定和几何体体积计算,属于中档题.

| A. | 一定是正数 | B. | 一定是负数 | ||
| C. | 正数、负数都有可能 | D. | 有可能是零 |
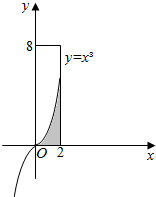 利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.
利用随机模拟方法计算y=x3和x=2以及x轴所围成的图形的面积.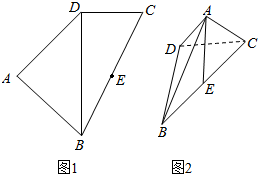 如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=$\sqrt{5}$,AB=AD=$\sqrt{2}$,将(图1)沿直线BD折起,使二面角A-BD-C成锐二面角且三棱锥A-BDC的体积为$\frac{\sqrt{3}}{6}$.(如图2)
如图,四边形ABCD中(图1),E是BC的中点,DB=2,DC=1,BC=$\sqrt{5}$,AB=AD=$\sqrt{2}$,将(图1)沿直线BD折起,使二面角A-BD-C成锐二面角且三棱锥A-BDC的体积为$\frac{\sqrt{3}}{6}$.(如图2)