题目内容
14.已知点A(3,2),点M到F($\frac{1}{2}$,0)的距离比它到y轴的距离大$\frac{1}{2}$.(1)求点M的轨迹方程;
(2)是否存在M,使|MA|+|MF|取得最小值?若存在,求此时点M的坐标;若不存在,请说明理由.
分析 (1)设出M坐标(x,y),当x≥0时由题意列出满足条件的等式,化简后得到M的轨迹方程;再由题意得到x轴负半轴上的点也满足条件.两种情况结合一起得到点M的轨迹方程.
(2)把|MF|+|MA|转化为|MA|+|PM|,利用当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2=2x 解得x值,即得M的坐标.
解答 解:(1)设M(x,y),则|MF|=$\sqrt{(x-\frac{1}{2})^{2}+{y}^{2}}$,
当x≥0时,M到y轴的距离为x.
由M到点F($\frac{1}{2}$,0)的距离比它到y轴的距离大$\frac{1}{2}$,得$\sqrt{(x-\frac{1}{2})^{2}+{y}^{2}}$=x+$\frac{1}{2}$.
两边平方并整理得:y2=2x;
当x<0时,由题意可得M的轨迹为y=0(x<0),此时符合题意.
综上,点M的轨迹方程为y2=2x或y=0(x<0).
(2)设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,
故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-$\frac{1}{2}$)=$\frac{7}{2}$.
把 y=2代入抛物线y2=2x 得 x=2,故点M的坐标是(2,2).
点评 本题考查了轨迹方程的求法,考查抛物线的定义和性质应用,解答的关键是不要漏掉x轴负半轴,利用抛物线定义,体现了转化的数学思想,是中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
9.已知直线l1,l2,l3的斜率分别是k1,k2,k3,其中l1∥l2,且k1,k3是方程2x2-3x-2=0的两根,则k1+k2+k3的值是( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | 1或$\frac{7}{2}$ |
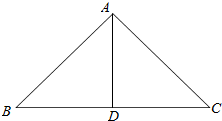 如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.
如图:已知△ABC中,∠BAD=∠C,AB=4,BD=2,$\overrightarrow{BD}$=$\overrightarrow{m}$.