题目内容
19.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,求:(1)$\overrightarrow{a}$•$\overrightarrow{b}$;
(2)$\overrightarrow{a}$2-$\overrightarrow{b}$2;
(3)(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$+3$\overrightarrow{b}$);
(4)|$\overrightarrow{a}$+$\overrightarrow{b}$|.
分析 (1)运用向量数量积的定义,计算即可得到;
(2)由向量的平方即为模的平方,即可得到所求值;
(3)将式子展开,由向量数量积的性质,即可得到所求值;
(4)运用向量的平方即为模的平方,即可得到所求值.
解答 解:(1)|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,
即有$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos60°=2×3×$\frac{1}{2}$=3;
(2)$\overrightarrow{a}$2-$\overrightarrow{b}$2=|$\overrightarrow{a}$|2-|$\overrightarrow{b}$|2=22-32=-5;
(3)(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$+3$\overrightarrow{b}$)=2$\overrightarrow{a}$2+3$\overrightarrow{b}$2+7$\overrightarrow{a}$•$\overrightarrow{b}$
=2×22+3×32+7×3=56;
(4)|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{4+9+2×3}$=$\sqrt{19}$.
点评 本题考查向量数量积的定义和性质,考查运算能力,属于基础题.

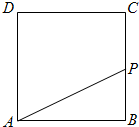 如图所示,在边长为4的正方形ABCD的边上有一点P,当P点由点B(起点)向点A(终点)沿逆时针方向移动(B→C→D→A)时,三点A、B、P构成△ABP,求:
如图所示,在边长为4的正方形ABCD的边上有一点P,当P点由点B(起点)向点A(终点)沿逆时针方向移动(B→C→D→A)时,三点A、B、P构成△ABP,求: