题目内容
凸四边形 中,其中
中,其中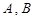 为定点,
为定点, 为动点,
为动点,
满足 .
.
(1)写出 与
与 的关系式;
的关系式;
(2)设 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值。
的最大值。
(1)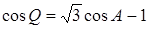 ;(2)
;(2)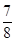
解析试题分析:(1)在三角形BCD和三角形BCD中,利用余弦定理表示出BD2,两者相等表示即可得到cosC与cosA的关系式;
(2)利用三角形面积公式变形出S与T,进而表示出S2+T2,将第一问表示出的cosA代入得到关于cosC的二次函数,利用二次函数性质即可求出S2+T2的最大值.
(1)在⊿PAB中,由余弦定理得: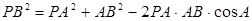
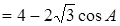 3分
3分
同理在⊿PQB中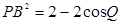 ∴
∴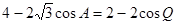
∴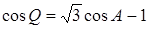 6分
6分
(2) 8分
8分
∴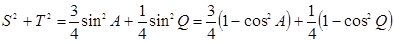
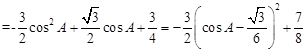
当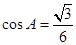 时,
时, 。 12分
。 12分
考点:1.余弦定理;2.三角形面积;3.同角三角函数间的基本关系以及二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 的值.
的值. ,
, ,且
,且 ∥
∥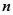 ,其中
,其中 是
是 的内角.
的内角. ,求
,求 的最大值.
的最大值. ,
, ,
, 分别为
分别为 三个内角
三个内角 ,
, ,
, 的对边,
的对边, 

 ,
,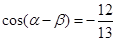 ,
,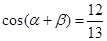 ,且
,且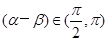 ,
,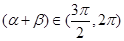 ,求角
,求角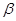 的值.
的值. ,且
,且 、
、 是方程
是方程 的两个根.
的两个根. 的值;
的值;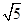 ,求△ABC的面积.
,求△ABC的面积. ,则
,则 = .
= . ,x∈R,且
,x∈R,且 .
. ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值. tan20°tan40°.
tan20°tan40°.