题目内容
已知曲线 的参数方程为
的参数方程为 (
(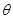 为参数),曲线
为参数),曲线 的极坐标方程
的极坐标方程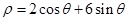 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)曲线 ,
, 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
(Ⅰ) 和
和 ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)参数方程化为普通方程,消去参数即可,极坐标方程化为直角坐标方程,利用两者坐标之间的关系互化,此类问题一般较为容易;(Ⅱ)由(Ⅰ)知,两曲线都是圆,判断两圆的位置关系,利用圆心距与两半径大小关系判断即可,两圆相交,公共弦和易求.
试题解析:(Ⅰ)由 消去参数
消去参数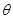 ,得
,得 的普通方程为:
的普通方程为: ;
;
由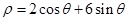 ,得
,得 ,化为直角坐标方程为
,化为直角坐标方程为 即
即 . 5分
. 5分
(Ⅱ)∵圆 的圆心为
的圆心为 ,圆
,圆 的圆心为
的圆心为
∴ ,∴两圆相交
,∴两圆相交
设相交弦长为 ,因为两圆半径相等,所以公共弦平分线段
,因为两圆半径相等,所以公共弦平分线段
∴
∴ ∴公共弦长为
∴公共弦长为 10分
10分
考点:极坐标方程和参数方程.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 (θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2: (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离. (φ为参数)的右焦点,且与直线
(φ为参数)的右焦点,且与直线 (t为参数)平行的直线的普通方程.
(t为参数)平行的直线的普通方程.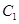 的参数方程是
的参数方程是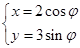 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线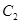 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在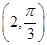 .
. 的取值范围.
的取值范围. 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为: ,曲线C2的参数方程为:
,曲线C2的参数方程为: ,点N的极坐标为
,点N的极坐标为 .
. 的取值范围.
的取值范围. 的参数方程为
的参数方程为 (
( 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
. 的参数方程为
的参数方程为
 为参数).若以坐标原点
为参数).若以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则曲线
轴正半轴为极轴建立极坐标系,则曲线 的极坐标方程为
的极坐标方程为 .
.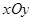 中,曲线
中,曲线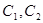 的参数方程分别为
的参数方程分别为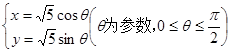 和
和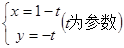 ,则曲线
,则曲线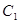 与
与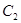 的交点坐标为
的交点坐标为  ,(t为参数),求直线的斜率.
,(t为参数),求直线的斜率.