题目内容
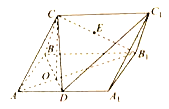
【题目】如图，四棱锥
的底面
是菱形，
与
交于点
，
底面，点
为线段
中点，
.
（1）求直线
与
所成角的正弦值；
（2）求平面
与平面
所成二面角的正弦值．
【答案】（1）
（2）
【解析】
（1）建立空间坐标系分别求得直线DP和BM的方向向量，进而得到异面直线的夹角；（2）分别求两个平面的法向量，再由向量夹角的计算公式得到结果.
（1）因为
是菱形，所以
．又
底面，以
为原点，直
分别为
轴，
轴，
轴，建立如图所示空间直角坐标系．
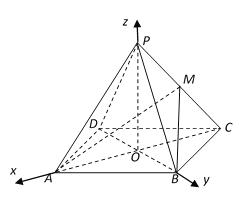
则
,
,
,
,
,
．
所以
，
，
，
，
．
则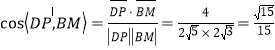
故直线
与
所成角的余弦值为
.
直线与所成角的正弦值为
.
（2）
，．．
设平面
的一个法向量为
，
则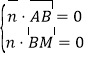
，得
，令
，得
，
．
得平面的一个法向量为
又,
设平面
的一个法向量为
，
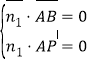得
，令
，得
，
．
得平面的一个法向量为
．
所以
，
，
．
则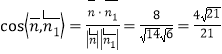
故平面与平面所成二面角的正弦值为.
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
【题目】从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：
质量指标值分组 | [75，85) | [85，95) | [95，105) | [105，115) | [115，125) |
频数 | 6 | 26 | 38 | 22 | 8 |
（I）在答题卡上作出这些数据的频率分布直方图：
（II）估计这种产品质量指标值的平均数及方差（同一组中的数据用该组区间的中点值作代表）；
（III）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？
【题目】“中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表：
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
.
(1)请将上面的列联表补充完整(直接写结果，不需要写求解过程)，并据此资料分析反感“中国式过马路”与性别是否有关？
(2)若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．
附：K2＝
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
