题目内容
16.定义区间[m,n]的长度为n-m,已知函数f(x)=x2+1的定义域为区间[a,b],值域为区间[1,10].求区间[a,b]长度的最大值和最小值.分析 可令y=1,解得x=0,令y=10,可得x=±3,结合二次函数的图象和性质,及区间的长度,即可得到结论.
解答 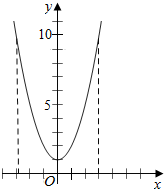 解:函数f(x)=x2+1,
解:函数f(x)=x2+1,
可令y=1,求得x=0,
再令y=10,可得x=±3,
则区间[a,b]长度最大的为[-3,3],其长度为6;
区间[a,b]长度最小的为[-3,0]或[0,3],其长度为3.
点评 本题考查二次函数的值域和定义域的关系,考查新定义的理解和运用,属于中档题.

练习册系列答案
相关题目
6.已知定义在R上的函数f(x)满足f(x)=2f(-x)+x2-2x,则函数( )
| A. | 有最大值0 | B. | 有最大值$\frac{1}{9}$ | C. | 有最小值0 | D. | 有最小值$\frac{1}{9}$ |
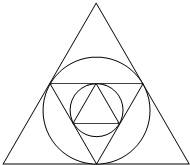 如图所示,作边长为a的正三角形的内切圆,在这个圆内作内接正三角形,然后,再作新三角形的内切圆,如此下去,求前n个内切圆的面积和.
如图所示,作边长为a的正三角形的内切圆,在这个圆内作内接正三角形,然后,再作新三角形的内切圆,如此下去,求前n个内切圆的面积和.