题目内容
本题满分14分)
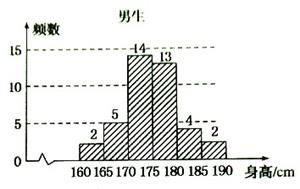
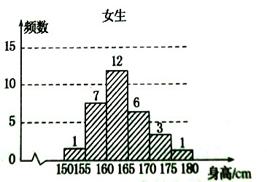
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男 生身高频数分布表
生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;
(2)估计该校学生身高(单位:cm)在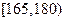 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在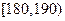 的男生中任选3人,设
的男生中任选3人,设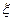 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在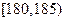 的人数,求
的人数,求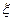 的分布列和数学期望.
的分布列和数学期望.
(1)直方图略
(2)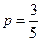
(3)分布列略 期望2
解析解(1)样本中男生人数为40 ,由分层抽样比例为10%可得全校男生人数为400--2分
频率分布直方图如图示:-----------------------------------------6分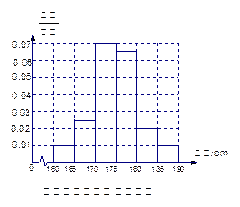
(2)由表1、表2知,样本中身高在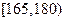 的学生人数为:
的学生人数为:
5+14+13+6+3+1=42,样本容量为70 ,所以样本中
学生身高在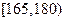 的频率
的频率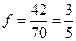
 ----8分
----8分
故由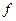 估计该校学生身高在
估计该校学生身高在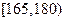 的概率
的概率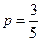 .-9分
.-9分
(3)依题意知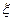 的可能取值为:1,2,3
的可能取值为:1,2,3
∵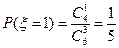 ,
,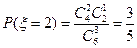 ,
,
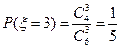 ----------------------------12分
----------------------------12分
∴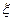 的分布列为:
的分布列为: ---------------------------13分
---------------------------13分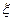 的数学期望
的数学期望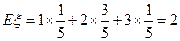 .------
.------ -----------
----------- ---------------14分
---------------14分

 阅读快车系列答案
阅读快车系列答案某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
(Ⅱ) 求单位成本y与月产量x之间的线性回归方程。(其中已计算得:
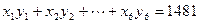 ,结果保留两位小数)
,结果保留两位小数) (本题14分)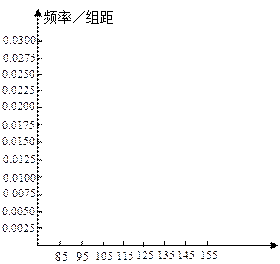 高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
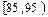 | ① | 0. 025 |
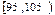 | | 0.050 |
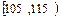 | | 0.200 |
 | 12 | 0.300 |
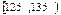 | | 0.275 |
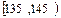 | 4 | ② |
| [145,155] | | 0.050 |
| 合计 | | ③ |
|
(1)根据上面图表,①②③处的数值分别为 ▲ 、 ▲ 、 ▲ ;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体落在[125,155]中的概率.
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| | 爱看课外书 | 不爱看课外书 | 总计 |
作文水平 好 好 | | | |
| 作文水平一般 | [来源:学。科。网Z。X。X。K] | | |
| 总计 | | | |
 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.参考公式:
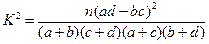 ,其中
,其中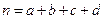 .
.参考数据:
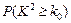 [来源:学*科*网] [来源:学*科*网] | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | X | 1 |
| B | 36 | y |
| C | 54 | 3 |
(2)若从高校A,C 抽取的人中选2人作专题发言,求这两人都来自高校C的概率.



 三分别抽取学生的人数;
三分别抽取学生的人数;