题目内容
某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月 份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量x千件 | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本y元/件 | 73 | 72 | 71 | 73 | 69 | 68 |
(Ⅱ) 求单位成本y与月产量x之间的线性回归方程。(其中已计算得:
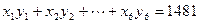 ,结果保留两位小数)
,结果保留两位小数)
(Ⅰ) 略
(Ⅱ) 已计算得: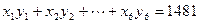 ,
,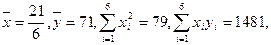

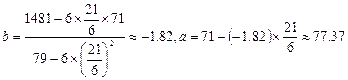
故线性回归方程为: .
.
解析

练习册系列答案
相关题目
(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
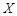 ,求
,求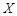 的分布列和期望;
的分布列和期望;(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
参考公式:
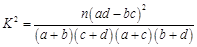 ,其中
,其中
参考数据:
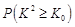 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
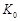 | 2.072 | 2.706 | 3.841 | 5.042 | 6.635 |
下表是关于某设备的使用年限(年)和所需要的维修费用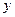 (万元)的几组统计数据:
(万元)的几组统计数据:
 | 2 | 3 | 4 | 5 | 6 |
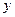 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)请根据上表提供的数据,用最小二乘法求出
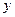 关于
关于 的线性回归方程
的线性回归方程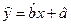 ;
;
(3)估计使用年限为10年时,维修费用为多少?
(参考数值或公式


、为加大西部开发步伐,国家支持西部地区选拔优秀“村官”深入农村开展工作,某市在2010年的“村官”选拔考试中随机抽取100名考生的成绩,按成绩分组,得到的频率分布表如下图所示:
(1)请先求出频率分布表中①、②位置的相应数据,再完成 下面的频率分布直方图;
下面的频率分布直方图;
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  | 5 | 0.05 |
| 第二组 |  | ① | 0.35 |
| 第三组 | 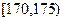 | 30 | ② |
| 第四组 |  | 20 | 0.20 |
| 第五组 |  | 10 | 0.10 |
| 合计 | 100 | 1.00 | |

(2)为了能够选拔出最优秀的“村官”到农村一线,市委组织部决定在笔试成绩高的第三、四、五组中
 用分层抽样抽取6名考生进入第二轮面试,求第3,4,5组每组各抽取多少考生进入第二轮面试?
用分层抽样抽取6名考生进入第二轮面试,求第3,4,5组每组各抽取多少考生进入第二轮面试? (本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了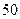 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的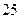 人中有
人中有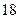 人作文水平好,另
人作文水平好,另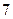 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的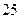 人中有
人中有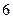 人作文水平好,另
人作文水平好,另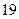 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个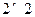 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为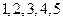 ,某
,某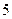 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为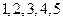 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附: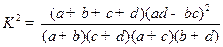
临界值表:
 | 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
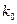 | 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
 意
意 击量,得如右所示的统计图,根据统计图:
击量,得如右所示的统计图,根据统计图: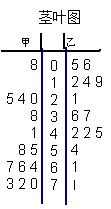
 量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多. 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系? ,
, ,可能用到数据:
,可能用到数据: ,
, ,
, ,
, .)
.)
 生身高频数分布表
生身高频数分布表

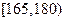 的概率;
的概率;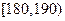 的男生中任选3人,设
的男生中任选3人,设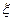 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在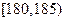 的人数,求
的人数,求