题目内容
19.已知圆C1:x2+y2-2mx+4y+m2-5=0与圆C2:x2+y2+2x-2my+m2-3=0.当m为何值时:(1)两圆外切?
(2)两圆内切?
分析 (1)将圆C1与圆C2分别化成标准形式,可得它们的圆心坐标和半径长.如果C1与C2外切,则两圆的半径之和等于它们圆心间的距离,由此建立关于m的方程,解之即可得到m的值;
(2)若C1与C2内切,则两圆的圆心距等于它们半径之差的绝对值,由此建立关于m的不等式,即可解出m的取值范围.
解答 解:∵圆C1:x2+y2-2mx+4y+m2-5=0,∴将圆C1化成标准方程,得
C1:(x-m)2+(y+2)2=9,圆心为C1(m,-2),半径r1=3
同理,C2的标准方程是:(x+1)2+(y-m)2=4,圆心为C2(-1,m),半径r2=2.
(1)如果圆C1与圆C2外切,则|C1C2|=r1+r2=5,即$\sqrt{(-1-m)^{2}+(m+2)^{2}}$=5
平方化简整理,得m2+3m-10=0,解之得m=2或-5;
(2)如果圆C1与圆C2外切,则|C1C2|=r1-r2=1,即$\sqrt{(-1-m)^{2}+(m+2)^{2}}$=1
平方化简整理,得m2+3m+2=0,解之得m=-2或-1.
点评 本题给出两个含有字母m的圆的一般方程,在满足外切、内切的情况下求m的取值范围.着重考查了圆的标准方程、两点间的距离公式和圆与圆的位置关系等知识,属于基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
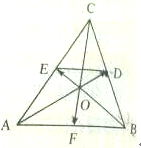 如图所示,已知△ABC中,D,E,F分别是BC,CA,AB的中点.且AD与BE交于O点.求证:$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{0}$.
如图所示,已知△ABC中,D,E,F分别是BC,CA,AB的中点.且AD与BE交于O点.求证:$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{0}$.