题目内容
已知a,b,c为正实数,a+b+c=1. 求证:
(1)a2+b2+c2≥
(2) ≤6
≤6
(1)a2+b2+c2≥

(2)
 ≤6
≤6证明略
(1)证法一:a2+b2+c2- =
= (3a2+3b2+3c2-1)
(3a2+3b2+3c2-1)
= [3a2+3b2+3c2-(a+b+c)2]
[3a2+3b2+3c2-(a+b+c)2]
= [3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]
[3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]
= [(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
[(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
证法二:∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
≤a2+b2+c2+a2+b2+a2+c2+b2+c2
∴3(a2+b2+c2)≥(a+b+c)2="1 " ∴a2+b2+c2≥
证法三: ∵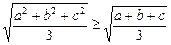 ∴a2+b2+c2≥
∴a2+b2+c2≥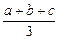
∴a2+b2+c2≥
证法四:设a= +α,b=
+α,b= +β,c=
+β,c= +γ.
+γ.
∵a+b+c=1,∴α+β+γ=0
∴a2+b2+c2=( +α)2+(
+α)2+( +β)2+(
+β)2+( +γ)2
+γ)2
= +
+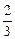 (α+β+γ)+α2+β2+γ2
(α+β+γ)+α2+β2+γ2
= +α2+β2+γ2≥
+α2+β2+γ2≥
∴a2+b2+c2≥

∴原不等式成立.
证法二: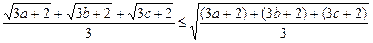
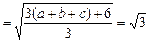
∴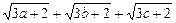 ≤
≤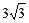 <6
<6
∴原不等式成立.
 =
= (3a2+3b2+3c2-1)
(3a2+3b2+3c2-1)=
 [3a2+3b2+3c2-(a+b+c)2]
[3a2+3b2+3c2-(a+b+c)2]=
 [3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]
[3a2+3b2+3c2-a2-b2-c2-2ab-2ac-2bc]=
 [(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
[(a-b)2+(b-c)2+(c-a)2]≥0 ∴a2+b2+c2≥
证法二:∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
≤a2+b2+c2+a2+b2+a2+c2+b2+c2
∴3(a2+b2+c2)≥(a+b+c)2="1 " ∴a2+b2+c2≥

证法三: ∵
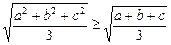 ∴a2+b2+c2≥
∴a2+b2+c2≥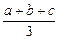
∴a2+b2+c2≥

证法四:设a=
 +α,b=
+α,b= +β,c=
+β,c= +γ.
+γ.∵a+b+c=1,∴α+β+γ=0
∴a2+b2+c2=(
 +α)2+(
+α)2+( +β)2+(
+β)2+( +γ)2
+γ)2=
 +
+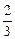 (α+β+γ)+α2+β2+γ2
(α+β+γ)+α2+β2+γ2=
 +α2+β2+γ2≥
+α2+β2+γ2≥
∴a2+b2+c2≥


∴原不等式成立.
证法二:
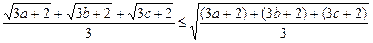
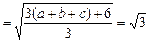
∴
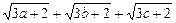 ≤
≤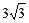 <6
<6∴原不等式成立.

练习册系列答案
相关题目
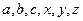 满足
满足 ,求证
,求证
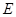 中,已知
中,已知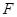 ,
,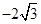 ,
,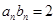 (
(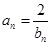 ,
,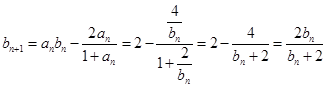 ).
).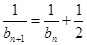 ,
,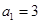 时,分别求
时,分别求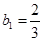 的值,判断
的值,判断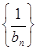 是否为定值,并给出证明;
是否为定值,并给出证明;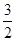 ,使得
,使得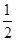 为完全平方数.
为完全平方数.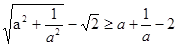
 ,求证:
,求证: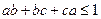 .
. .
.
 的单调区间;
的单调区间;
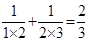 ,
,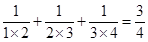 ,
, 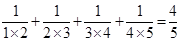 ,根据以上规律,写出第四个等式为:__________.
,根据以上规律,写出第四个等式为:__________.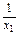 +
+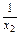 +…+
+…+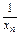 ≥n2.
≥n2.