题目内容
【题目】已知Sn是正项数列{an}的前n项和,满足a1=2,anan+1=6Sn﹣2,n∈N*.
(1)求证:{an}是等差数列;
(2)记bn=2n,求数列{|an﹣bn|}的前n项和Tn.
【答案】(1)见解析(2)Tn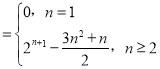 .
.
【解析】
(1)由anan+1=6Sn﹣2当n≥2时,有an﹣1an=6Sn﹣1﹣2,两式相减得an+1﹣an﹣1=6,再由数列的前几项推证出结果;
(2)由(Ⅰ)可得an=3n﹣1,记cn=bn﹣an,研究其单调性,判断其符号,再求前n项和Tn.
解:(1)证明:∵a1=2,anan+1=6Sn﹣2①, ∴当n≥2时,有an﹣1an=6Sn﹣1﹣2②,
由①﹣②整理得an+1﹣an﹣1=6,
∴数列{an}的奇数项、偶数项均是公差为6的等差数列,
又由题设条件可得a1=2,a2=5,a3=8,a4=11,
所以an+1﹣an=3,故数列{an}是首项为2,公差为3的等差数列;
(2)解:由(Ⅰ)可得an=3n﹣1,又bn=2n,记![]() ,
,
∴当n≥2时,cn单调递增,且c1=0,c2=﹣1,c3=0,从第4项起,cn>0,
∴当n=1时,有T1=0;当n=2时,有T2=1;
当n≥3时,有Tn=﹣c1﹣c2+c3+c4+…+cn=1+(23+24+…+2n)+n﹣2﹣3(3+4+5+…+n)
=n﹣1![]() 3
3![]() =2n+1
=2n+1![]() ,
,
故Tn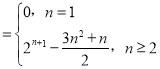 .
.

【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
内,则为合格品,否则为不合格品.图1是甲套设备的样本的频率分布直方图,表1是乙套设备的样本的频数分布表.
图1:甲套设备的样本的频率分布直方图
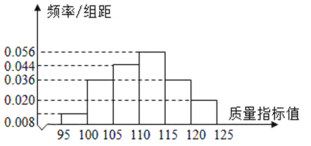
表1:乙套设备的样本的频数分布表
质量指标数 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;
(2)填写下面列联表,并根据列联表判断是否有95%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备 | 乙套设备 | 合计 | |
合格 | |||
不合格 | |||
合计 |
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]() 其中
其中![]()