题目内容
，求
。
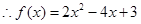
解析试题分析：1）题意分析：已知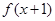
，求
2）解题思路：换元法
解：令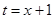
，则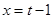
，
。。
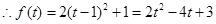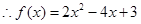考点：函数的解析式
点评：凡是已知
，求的题型，均可用换元法求解，在换元的过程中要注意新元的取值范围
练习册系列答案
小题狂做系列答案
相关题目
小题狂做系列答案题目内容
，求。
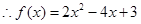
解析试题分析：1）题意分析：已知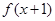，求
2）解题思路：换元法
解：令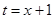，则，。。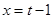
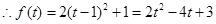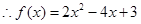考点：函数的解析式
点评：凡是已知，求的题型，均可用换元法求解，在换元的过程中要注意新元的取值范围
小题狂做系列答案
时，求函数
的值域；
，+
的高考资源网取值范围.
，且对任意的实数
都有
成立.
的值；
在区间
上是增函数.
为实数，
，
，求
的单调区间；
，求
的最大值．
的函数
是奇函数。
的值；
的奇偶性；
是增函数，求实数
的取值范围。
的最小正周期.
时，求函数
在
上为增函数，求正实数
的取值范围；
时，求
上的最大值和最小值；
，都有
。