题目内容
解不等式:|x+1|+|x-2|<x2+1.
【答案】分析:对x≤-1、-1<x<2、x≥2分别去掉绝对值符号,然后解二次不等式,取并集即可.
解答:解:当x≤-1时,原不等式可化为:-(x+1)-(x-2)<x2+1,
解得:x<-2或x>0.
∴x<-2.(3分)
当-1<x<2时,原不等式可化为:(x+1)-(x-2)<x2+1,
解得:x<-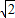 或
或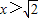
∴ .(5分)
.(5分)
当x≥2时,原不等式可化为:(x+1)+(x-2)<x2+1,解得x∈R.
∴x≥2.(8分)
综上所述,原不等式的解集为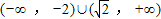 .(10分)
.(10分)
点评:本题考查绝对值不等式的解法,考查分类讨论思想,是基础题.
解答:解:当x≤-1时,原不等式可化为:-(x+1)-(x-2)<x2+1,
解得:x<-2或x>0.
∴x<-2.(3分)
当-1<x<2时,原不等式可化为:(x+1)-(x-2)<x2+1,
解得:x<-
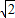 或
或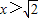
∴
 .(5分)
.(5分)当x≥2时,原不等式可化为:(x+1)+(x-2)<x2+1,解得x∈R.
∴x≥2.(8分)
综上所述,原不等式的解集为
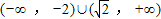 .(10分)
.(10分)点评:本题考查绝对值不等式的解法,考查分类讨论思想,是基础题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目