题目内容
14.已知集合A={x|x2-4x-5≥0},集合B={x|2a≤x≤a+2}.(1)若a=-1,求A∩B,A∪B;
(2)若A∩B=B,求实数a的取值范围.
分析 (1)由此能求出集合A={x|x2-4x-5≥0}={x|x≤-1或x≥5},从而能求出A∩B和A∪B.
(2)由A∩B=B,得B⊆A,由此能求出实数a的取值范围.
解答 解:(1)a=-1时,集合A={x|x2-4x-5≥0}={x|x≤-1或x≥5},
集合B={x|2a≤x≤a+2}={x|-2≤x≤1},
∴A∩B={x|-2≤x≤-1},
A∪B={x|x≤1或x≥5}.
(2)∵A∩B=B,∴B⊆A,
当B=∅时,2a>a+2,解得a>2;
当B≠∅时,$\left\{\begin{array}{l}{a≤2}\\{a+2≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{a≤2}\\{2a≥5}\end{array}\right.$,
解得a≤-3.
综上,a>2或a≤-3.
点评 本题考查交集和并集的求法,是基础题,解题时要认真审题,注意不等式性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
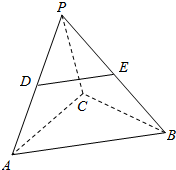 已知在三棱锥P-ABC中,D,E分别是PA,PB上的点,DE∥平面ABC,求证:$\frac{PD}{PA}=\frac{PE}{PB}$.
已知在三棱锥P-ABC中,D,E分别是PA,PB上的点,DE∥平面ABC,求证:$\frac{PD}{PA}=\frac{PE}{PB}$.