题目内容
6．
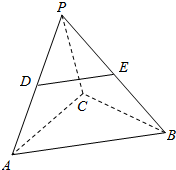已知在三棱锥P-ABC中，D，E分别是PA，PB上的点，DE∥平面ABC，求证：$\frac{PD}{PA}=\frac{PE}{PB}$．
分析 根据DE∥平面ABC，得出DE∥AB，从而证明$\frac{PD}{PA}=\frac{PE}{PB}$．
解答 证明：三棱锥P-ABC中，∵DE∥平面ABC，
且DE?平面PAB，AB?平面PAB，
∴DE∥AB；
∴$\frac{PD}{PA}=\frac{PE}{PB}$．
点评 本题考查了空间中的线面平行转化为线线平行以及平行线截得对应线段成比例的应用问题，是基础题目．
练习册系列答案
相关题目
16．函数y=lgx+x有零点的区间是（ ）
| A． | （1，2） | B． | （$\frac{1}{10}，1$） | C． | （2，3） | D． | （-∞，0） |
17．已知α∈$（0，\frac{π}{2}）$，β∈$（\frac{π}{2}，π）$，且sinα＞sinβ，则α与β的关系是（ ）
| A． | 0＜β+α＜$\frac{π}{2}$ | B． | $\frac{π}{2}$＜α+β＜π | C． | π＜α+β＜$\frac{3}{2}$π | D． | $\frac{π}{2}$＜α+β＜$\frac{3}{2}$π |
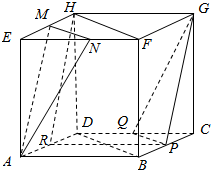如图，在正方体ABCD-EFGH中，M，N，P，Q，R分别是EH，EF，BC，CD，AD的中点，求证：平面MNA∥平面PQG．