题目内容
若干个能唯一确定一个数列的量称为该数列的“基量”.{an}是公比为q的无穷等比数列,下列“基量”为 组;(1)S1与S2;(2)a2与S3;(3)a1与an;(4)q与an(n为大于1的整数,Sn为{an}的前n项和)
【答案】分析:(1)利用S1和S2,可知a1和a2.由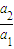 可得公比q,从而可判断
可得公比q,从而可判断
(2)由a2与S3,设其公比为q,首项为a1,可得把a1和q代入等比数列的通项公式和求和公式,判断q是否唯一确定,
(3)a1与an,可得an=a1qn-1,当n为奇数时,q可能有两个值,从而可判断
(4)由通项公式,数列{an} 能够确定,从而可判断
解答:解:(1)由S1和S2,可知a1和a2.由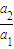 可得公比q,故能确定数列是该数列的“基本量”①对;
可得公比q,故能确定数列是该数列的“基本量”①对;
(2)由a2与S3,设其公比为q,首项为a1,可得把a2和S3代入等比数列的求和公式,
设其公比为q,首项为a1,可得a2=a1q,S3=a1+a1q+a1q2,满足条件的q可能不存在,也可能不止一个,因而不能确定数列,故不一定是数列 的基本量,故不对;
(3)由a1与an,可得an=a1qn-1,当n为奇数时,q可能有两个值,故不一定能确定数列,所以也不一定是数列的一个基本量.
(4)由q与an由a得an=a1qn-1,故数列{an} 能够确定,是数列{an} 的一个基本量;
故答案为(1)(4)
点评:本题主要考查等比数列的通项公式,求和公式及等比数列的性质.考查了学生分析问题和解决问题的能力
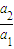 可得公比q,从而可判断
可得公比q,从而可判断(2)由a2与S3,设其公比为q,首项为a1,可得把a1和q代入等比数列的通项公式和求和公式,判断q是否唯一确定,
(3)a1与an,可得an=a1qn-1,当n为奇数时,q可能有两个值,从而可判断
(4)由通项公式,数列{an} 能够确定,从而可判断
解答:解:(1)由S1和S2,可知a1和a2.由
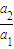 可得公比q,故能确定数列是该数列的“基本量”①对;
可得公比q,故能确定数列是该数列的“基本量”①对;(2)由a2与S3,设其公比为q,首项为a1,可得把a2和S3代入等比数列的求和公式,
设其公比为q,首项为a1,可得a2=a1q,S3=a1+a1q+a1q2,满足条件的q可能不存在,也可能不止一个,因而不能确定数列,故不一定是数列 的基本量,故不对;
(3)由a1与an,可得an=a1qn-1,当n为奇数时,q可能有两个值,故不一定能确定数列,所以也不一定是数列的一个基本量.
(4)由q与an由a得an=a1qn-1,故数列{an} 能够确定,是数列{an} 的一个基本量;
故答案为(1)(4)
点评:本题主要考查等比数列的通项公式,求和公式及等比数列的性质.考查了学生分析问题和解决问题的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 }是公比为q的无穷等比数列,下列{
}是公比为q的无穷等比数列,下列{ 与
与 ②
② 与
与 ③
③ 与
与 为{
为{