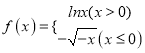题目内容
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且2cos2
·cosB－sin(A－B)sinB＋cos(A＋C)＝－
.
(1)求cos A的值；
(2)若a＝4
，b＝5，求
在
方向上的投影.
【答案】（1）－
（2）
【解析】
(1)由2cos2
cosB－sin(A－B)sinB＋cos(A＋C)＝－，得
[cos(A－B)＋1]cosB－sin(A－B)sinB－cosB＝－，
∴cos(A－B)cosB－sin(A－B)sinB＝－.
则cos(A－B＋B)＝－，即cosA＝－.
(2)由cosA＝－，0<A<π，得sinA＝
，
由正弦定理，有
，所以，sinB＝
.
由题知a>b，则A>B，故B＝
，
根据余弦定理，有(4
)2＝52＋c2－2×5c×
，
解得c＝1或c＝－7(舍去)．
故向量
在
方向上的投影为||cosB＝.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】已知椭圆的方程为
（
），其离心率
，
分别为椭圆的左、右焦点，
为椭圆上的点（不在
轴上），
周长为6.过椭圆右焦点
的直线
与椭圆交于
两点，
为坐标原点，
面积为
.
（1）求椭圆的标准方程：
（2）求直线的方程.
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对40名小学六年级学生进行了问卷调查，并得到如下列联表.平均每天喝
以上为“常喝”，体重超过
为“肥胖”.已知在全部40人中随机抽取1人，抽到肥胖学生的概率为
.
常喝 | 不常喝 | 合计 | |
肥胖 | 3 | ||
不肥胖 | 5 | ||
合计 | 40 |
（1）请将上面的列联表补充完整；
（2）是否有
的把握认为肥胖与常喝碳酸饮料有关？请说明你的理由.
参考公式：
①卡方统计量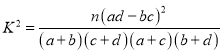
，其中
为样本容量；
②独立性检验中
的临界值参考表：
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
