题目内容
已知实数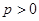 ,直线
,直线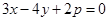 与抛物线
与抛物线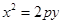 和圆
和圆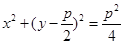 从左到右的交点依次为
从左到右的交点依次为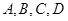 ,则
,则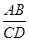 的值为 .
的值为 .

解析试题分析:直线方程与抛物线方程联立解得,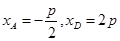 ,直线方程与圆方程联立解得,
,直线方程与圆方程联立解得,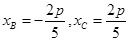 ,所以
,所以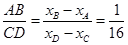 .
.
考点:曲线的方程、曲线的交点的求法.

练习册系列答案
相关题目
题目内容
已知实数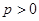 ,直线
,直线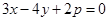 与抛物线
与抛物线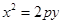 和圆
和圆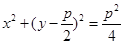 从左到右的交点依次为
从左到右的交点依次为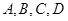 ,则
,则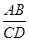 的值为 .
的值为 .

解析试题分析:直线方程与抛物线方程联立解得,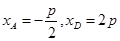 ,直线方程与圆方程联立解得,
,直线方程与圆方程联立解得,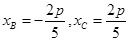 ,所以
,所以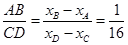 .
.
考点:曲线的方程、曲线的交点的求法.
