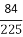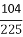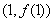题目内容
为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
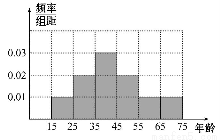
(1)作出被调查人员年龄的频率分布直方图.
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
(1)如图
(2) ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
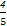
【解析】(1)各组的频率分别是0.1,0.2,0.3,0.2,0.1,0.1.
所以图中各组的纵坐标分别是:0.01,0.02,0.03,0.02,0.01,0.01.
则频率分布直方图如图.

(2)ξ所有可能取值有0,1,2,3,
P(ξ=0)=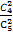 ·
·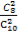 =
= ×
× =
=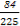 .
.
P(ξ=1)=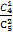 ×
×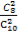 +
+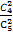 ×
×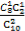 =
=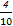 ×
× +
+ ×
×
=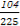 .
.
P(ξ=2)= ×
×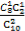 +
+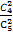 ×
×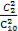 =
=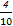 ×
× +
+ ×
×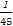
=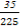 .
.
P(ξ=3)=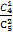 ·
·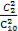 =
=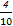 ×
×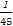 =
=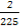 .
.
所以ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以ξ的期望值E(ξ)=0+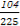 +
+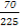 +
+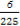 =
=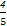 .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
由表中数据算出线性回归方程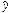 =bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a=
=bx+a中的b≈0.7,试预测加工10个零件需_______小时(已知a=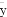 -b
-b ).
).