题目内容
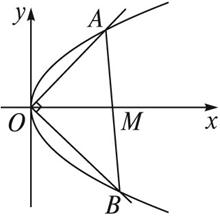
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为![]() 的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
的直线l与线段OA相交(不经过点O或点A)且交抛物线于M、N两点,求△AMN面积最大时直线l的方程,并求△AMN的最大面积.
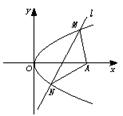
直线l的方程为y=x-1,△AMN的最大面积为8![]() .
.
解析:
由题意,可设l的方程为y=x+m,-5<m<0.
由方程组![]() ,消去y,得x2+(2m-4)x+m2=0 ①
,消去y,得x2+(2m-4)x+m2=0 ①
∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式Δ=(2m-4)2-4m2=16(1-m)>0,
解得m<1,又-5<m<0,∴m的范围为(-5,0)
设M(x1,y1),N(x2,y2)则x1+x2=4-2m,x1·x2=m2,
∴|MN|=4![]() .
.
点A到直线l的距离为d=![]() .
.
∴S△=2(5+m)![]() ,从而S△2=4(1-m)(5+m)2
,从而S△2=4(1-m)(5+m)2
=2(2-2m)·(5+m)(5+m)≤2(![]() )3=128.
)3=128.
∴S△≤8![]() ,当且仅当2-2m=5+m,即m=-1时取等号.
,当且仅当2-2m=5+m,即m=-1时取等号.
故直线l的方程为y=x-1,△AMN的最大面积为8![]() .
.

练习册系列答案
相关题目
 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为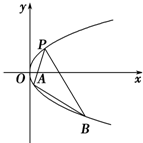 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为