题目内容
如图所示,过抛物线y2=2px的顶点O作两条互相垂直的弦交抛物线于A、B两点.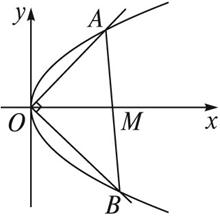
(1)证明直线AB过定点;
(2)求△AOB面积的最小值.
解:(1)设直线AB的方程为y=k(x-a),A(x1,y1),B(x2,y2).联立方程
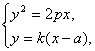 消去x得ky2-2py-2pak=0,
消去x得ky2-2py-2pak=0,
则y1y2=-2pa.又OA⊥OB.
∴y1y2=-x1x2.
由方程组消去y,得k2x2-(2k2a+2p)x+k2a2=0,则x1·x2=a2.因此,a2=2pa.∴a=2p.
故直线AB过定点(2p,0).
(2)由(1)知:AB恒过定点M(2p,0).
∴S△AOB=S△AOM+S△BOM=![]() |OM|(|y1|+|y2|)≥p(2
|OM|(|y1|+|y2|)≥p(2![]() |).
|).
又y12=2px1,y22=2px2,
∴(y1y2)2=4p2x1x2.
又∵y1y2=-x1x2,
于是|y1y2|=4p2.
故S△AOB的最小值为4p2.
绿色通道:
对于直线、曲线方程联立求解,灵活运用整体思想及韦达定理可简化解答;另外应注意图形的有效利用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为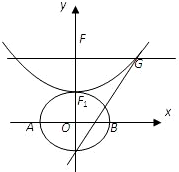 设b>0,椭圆方程为
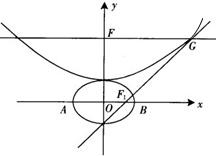
设b>0,椭圆方程为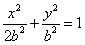 ,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,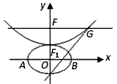
 设b>0,椭圆方程为
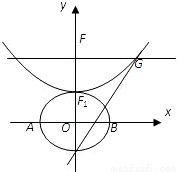
设b>0,椭圆方程为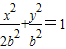 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.