题目内容
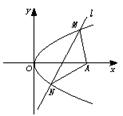
如图所示,抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与抛物线交于不同的两点A、B,

(1)若|AB|≤2p,求a的取值范围;
(2)若线段AB的垂直平分线交AB于点Q,交x轴于点N,求△MNQ的面积.
答案:
解析:
解析:
|
解析:(1)直线l的方程为y=x-a, 由 设直线l与抛物线的交点A(x1,y1),B(x2,y2), 则 因为0<|AB|≤2p,所以0<8p(p+2a)≤4p2,即 (2)设Q(x0,y0),得 |QM|= |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
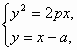 消y得x2-2(a+p)x+a2=0.
消y得x2-2(a+p)x+a2=0.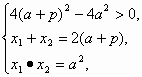 所以|AB|=
所以|AB|=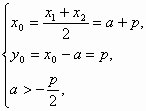
 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为