题目内容
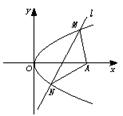
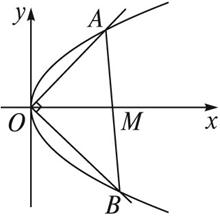
 如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为
如图所示,抛物线y2=4x的顶点为O,点A的坐标为(5,0),倾斜角为| π |
| 4 |
8
| 2 |
8
.| 2 |
分析:由题意,可设l的方程为y=x+m,其中-5<m<0,与抛物线的方程联立可得△>0即根与系数的关系,再利用弦长公式和点到直线的距离公式即可得到三角形的面积,再利用基本不等式即可得出其最大值.
解答: 解:由题意,可设l的方程为y=x+m,其中-5<m<0,
解:由题意,可设l的方程为y=x+m,其中-5<m<0,
由方程组
,消去y,得x2+(2m-4)x+m2=0,①
∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式△=(2m-4)2-4m2=16(1-m)>0,解得m<1,又-5<m<0,
∴m的范围为(-5,0),
设M(x1,y1),N(x2,y2),则x1+x2=4-2m,x1?x2=m2,
∴|MN|=
=
=4
,点A到直线的距离为d=
.
∴S△=2(5+m)
,
从而
=4(1-m)(5+m)2=2(2-2m)?(5+m)(5+m)≤2(
)3=128,
∴S△≤8
,当且仅当2-2m=5+m,即m=-1时取等号.
故直线l的方程为y=x-1,△AMN的最大面积为8
.
 解:由题意,可设l的方程为y=x+m,其中-5<m<0,
解:由题意,可设l的方程为y=x+m,其中-5<m<0,由方程组
|
∵直线l与抛物线有两个不同交点M、N,
∴方程①的判别式△=(2m-4)2-4m2=16(1-m)>0,解得m<1,又-5<m<0,
∴m的范围为(-5,0),
设M(x1,y1),N(x2,y2),则x1+x2=4-2m,x1?x2=m2,
∴|MN|=
| (1+12)[(x1+x2)2-4x1x2] |
| 2[(4-2m)2-4m2] |
| 2(1-m) |
| 5+m | ||
|
∴S△=2(5+m)
| 1-m |
从而
| S | 2 △ |
| 2-2m+5+m+5+m |
| 3 |
∴S△≤8
| 2 |
故直线l的方程为y=x-1,△AMN的最大面积为8
| 2 |
点评:本题考查了直线与抛物线相交问题转化为方程联立可得△>0即根与系数的关系、弦长公式和点到直线的距离公式、三角形的面积、基本不等式等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
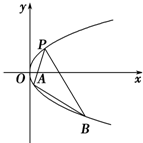 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为