题目内容
(本小题满分12分)
设锐角三角形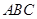 的内角
的内角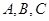 的对边分别为
的对边分别为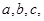
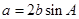
(I)求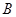 的大小;
的大小;
(II)若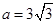 ,
,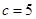 ,求
,求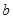 .
.
(I)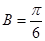 (II)
(II)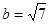
解析试题分析:(I)因为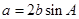 ,所以
,所以 ,
,
由正弦定理 ,可得
,可得 ,所以
,所以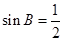 ,
,
又三角形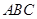 为锐角三角形,所以
为锐角三角形,所以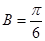 . ……6分
. ……6分
(II)因为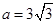 ,
,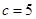 ,由(I)知
,由(I)知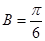 ,
,
所以由余弦定理得: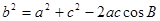
 ,
,
所以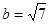 . ……12分
. ……12分
考点:本小题主要考查正弦定理、余弦定理在解三角形中的应用,考查学生的运算求解能力和思维的严谨性.
点评:在三角形中,要恰当选择正弦定理或是余弦定理,把边化成角或是把角化成边.需要特别注意的是求出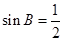 后,要强调
后,要强调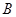 的取值范围才能得出
的取值范围才能得出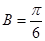 .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为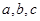 ,且满足
,且满足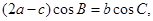

 的大小;
的大小; 的取值范围。
的取值范围。 中,
中, ,
, ,
,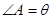 .
. 的表达式
的表达式 中,内角
中,内角 所对边的长分别为
所对边的长分别为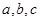 ,已知向量
,已知向量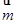 ="(1,cosA" -1),
="(1,cosA" -1),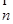 =(cosA,1)且满足
=(cosA,1)且满足 的大小;
的大小; ,求
,求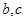 的值.
的值.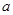 、
、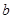 、
、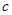 分别是
分别是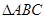 的三个内角
的三个内角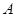 、
、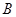 、
、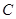 所对的边;
所对的边; ,且
,且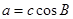 ,且
,且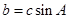 ,试判断
,试判断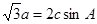
 ,且△ABC的面积为
,且△ABC的面积为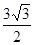
 ,求a+b的值。
,求a+b的值。 、
、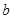 、
、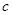 分别是
分别是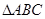 的三个内角
的三个内角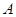 、
、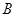 、
、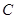 所对的边,(1)若
所对的边,(1)若 求
求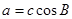 ,且
,且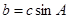 ,试判断
,试判断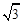 sin C.
sin C. 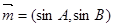 ,
,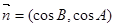 ,
,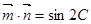 ,且
,且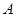 、
、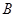 、
、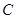 分别为
分别为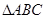 的三边
的三边 、
、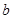 、
、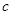 所对的角。
所对的角。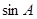 ,
,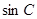 ,
,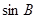 成等差数列,且
成等差数列,且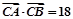 ,求
,求