题目内容
设椭圆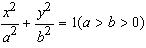 的左、右焦点分别是F1和F2,离心率e=
的左、右焦点分别是F1和F2,离心率e=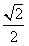 ,点F2到右准线l的距离为
,点F2到右准线l的距离为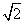 ,
,
(Ⅰ)求a、b的值;
(Ⅱ)设M、N是右准线l上两动点,满足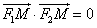 ,证明:当
,证明:当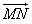 取最小值时,
取最小值时,
 。
。
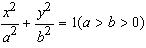 的左、右焦点分别是F1和F2,离心率e=
的左、右焦点分别是F1和F2,离心率e=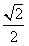 ,点F2到右准线l的距离为
,点F2到右准线l的距离为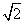 ,
,(Ⅰ)求a、b的值;
(Ⅱ)设M、N是右准线l上两动点,满足
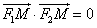 ,证明:当
,证明:当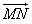 取最小值时,
取最小值时, 。
。解:(1)因为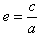 ,F2到l的距离
,F2到l的距离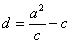 ,
,
所以由题设得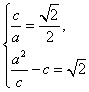 ,解得
,解得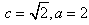 ,
,
由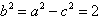 ,得b=
,得b=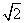 ;
;
(Ⅱ)由c=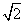 ,a=2得
,a=2得 ,
,
l的方程为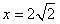 ,
,
故可设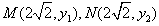 ,
,
由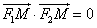 知
知 ,
,
得y1y2=-6,所以y1y2≠0,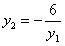 ,
,
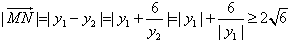 ,
,
当且仅当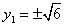 时,上式取等号,此时y2=-y1,
时,上式取等号,此时y2=-y1,
所以,
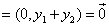 。
。
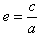 ,F2到l的距离
,F2到l的距离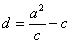 ,
,所以由题设得
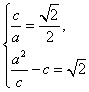 ,解得
,解得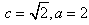 ,
,由
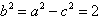 ,得b=
,得b=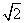 ;
;(Ⅱ)由c=
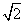 ,a=2得
,a=2得 ,
,l的方程为
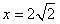 ,
,故可设
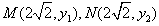 ,
,由
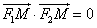 知
知 ,
,得y1y2=-6,所以y1y2≠0,
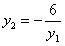 ,
,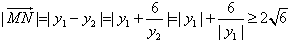 ,
,当且仅当
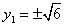 时,上式取等号,此时y2=-y1,
时,上式取等号,此时y2=-y1,所以,

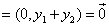 。
。
练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且 ,
, ,求a、b的值;
,求a、b的值; 最小时,求证
最小时,求证 与
与 共线。
共线。 
 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.