题目内容
设椭圆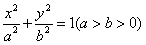 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率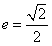 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且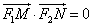 ,
,
(Ⅰ)若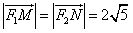 ,求a、b的值;
,求a、b的值;
(Ⅱ)当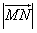 最小时,求证
最小时,求证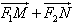 与
与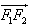 共线。
共线。
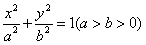 的左、右焦点分别是F1、F2,离心率
的左、右焦点分别是F1、F2,离心率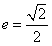 ,右准线l上的两动点M、N,且
,右准线l上的两动点M、N,且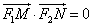 ,
,(Ⅰ)若
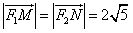 ,求a、b的值;
,求a、b的值;(Ⅱ)当
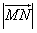 最小时,求证
最小时,求证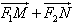 与
与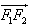 共线。
共线。 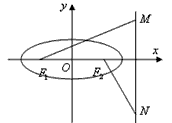
(Ⅰ)解:由已知, ,由
,由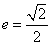 ,
,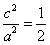 ,∴
,∴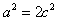 ,
,
又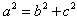 ,
,
∴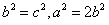 ,
,
∴l: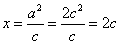 ,
,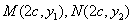 ,
,
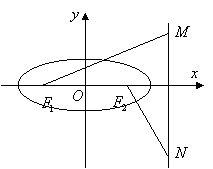
延长NF2交MF1于P,记右准线l交x轴于Q,
∵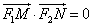 ,
,
∴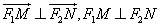 ,
,
由平面几何知识易证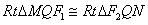 ,
,
∴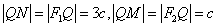 ,即
,即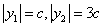 ,
,
∵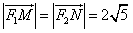 ,
,
∴ ,c2=2,b2=2,a2=4,
,c2=2,b2=2,a2=4,
∴a=2,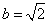 .
.
(Ⅱ)证明:∵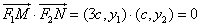 ,
,
∴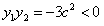 ,
,
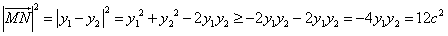 ,
,
当且仅当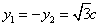 或
或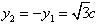 时,取等号,
时,取等号,
此时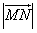 取最小值
取最小值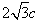 ,
,
此时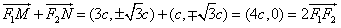 ,
,
∴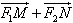 与
与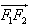 共线.
共线.
 ,由
,由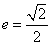 ,
,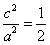 ,∴
,∴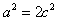 ,
,又
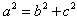 ,
,∴
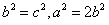 ,
, ∴l:
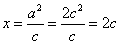 ,
,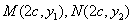 ,
,延长NF2交MF1于P,记右准线l交x轴于Q,
∵
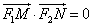 ,
,∴
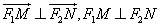 ,
,由平面几何知识易证
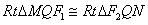 ,
,∴
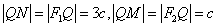 ,即
,即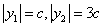 ,
, ∵
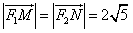 ,
,∴
 ,c2=2,b2=2,a2=4,
,c2=2,b2=2,a2=4,∴a=2,
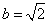 .
. (Ⅱ)证明:∵
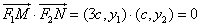 ,
,∴
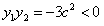 ,
,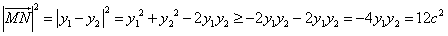 ,
,当且仅当
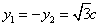 或
或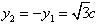 时,取等号,
时,取等号,此时
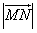 取最小值
取最小值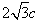 ,
,此时
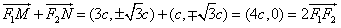 ,
,∴
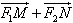 与
与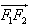 共线.
共线. 
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.
,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+2相切.