题目内容
(08年四川卷理)设椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,右准线
,右准线![]() 上的两动点
上的两动点![]() 、
、![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求
,求![]() 、
、![]() 的值;
的值;
(Ⅱ)当![]() 最小时,求证
最小时,求证![]() 与
与![]() 共线.
共线.

解析:数列和解几位列倒数第三和第二,意料之中.开始挤牙膏吧.
(Ⅰ)由已知,![]() ,
,![]() .由
.由![]() ,
,![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() :
:![]() ,
,![]() ,
,![]() .
.
延长![]() 交
交![]() 于
于![]() ,记右准线
,记右准线![]() 交
交![]() 轴于
轴于![]() .
.
∵![]() ,∴
,∴![]() .
.![]()
由平几知识易证![]() ≌
≌![]()
∴![]() ,
,![]()
即![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
(Ⅰ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
又![]()
联立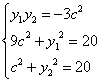 ,消去
,消去![]() 、
、![]() 得:
得:![]() ,
,
整理得:![]() ,
,![]() .解得
.解得![]() .但解此方程组要考倒不少人.
.但解此方程组要考倒不少人.
(Ⅱ)∵![]() ,∴
,∴![]() .
.
![]() .
.
当且仅当![]() 或
或![]() 时,取等号.此时
时,取等号.此时![]() 取最小值
取最小值![]() .
.
此时![]() .
.
∴![]() 与
与![]() 共线.
共线.
(Ⅱ)另解:∵![]() ,∴
,∴![]() ,
,![]() .
.
设![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
由![]() ,由
,由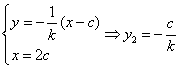
![]() .当且仅当
.当且仅当![]() 即
即![]() ,
,![]() 时取等号.
时取等号.
即当![]() 最小时,
最小时,![]() ,
,
此时![]() .
.
∴![]() 与
与![]() 共线.
共线.
点评:本题第一问又用到了平面几何.看来,与平面几何有联系的难题真是四川风格啊.注意平面几何可与三角向量解几沾边,应加强对含平面几何背景的试题的研究.本题好得好,出得活,出得妙!均值定理,放缩技巧,永恒的考点.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目