题目内容
已知向量 (m为常数),且
(m为常数),且 ,
, 不共线,若向量
不共线,若向量 ,
, 的夹角为锐角,求实数x的取值范围.
的夹角为锐角,求实数x的取值范围.
【答案】分析:只要
 >0且
>0且
 (λ∈R)即可,先表示出
(λ∈R)即可,先表示出
 >0再由
>0再由
 确定x的范围.
确定x的范围.
解答:解:要满足 ,
, 的夹角为锐角
的夹角为锐角
只须
 >0且
>0且
 (λ∈R),
(λ∈R),
 =
= =
= =
= 即x(mx-1)>0
即x(mx-1)>0
1°当m>0时x<0或
2°m<0时x(-mx+1)<0,
3°m=0时只要x<0
综上所述:m>0时,
m=0时,x∈(-∞,0)
m<0时, .
.
点评:本题主要考查两向量夹角的问题.两向量夹角为锐角时两向量点乘大于0且不共线,为钝角时两向量点乘小于0且不共线.

 >0且
>0且
 (λ∈R)即可,先表示出
(λ∈R)即可,先表示出
 >0再由
>0再由
 确定x的范围.
确定x的范围.解答:解:要满足
 ,
, 的夹角为锐角
的夹角为锐角只须

 >0且
>0且
 (λ∈R),
(λ∈R),
 =
= =
= =
= 即x(mx-1)>0
即x(mx-1)>01°当m>0时x<0或

2°m<0时x(-mx+1)<0,

3°m=0时只要x<0
综上所述:m>0时,

m=0时,x∈(-∞,0)
m<0时,
 .
.点评:本题主要考查两向量夹角的问题.两向量夹角为锐角时两向量点乘大于0且不共线,为钝角时两向量点乘小于0且不共线.

练习册系列答案
相关题目
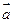 =(1,
=(1,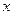 ),
),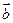 =(
=(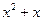 ,
,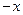 ),m为常数且m≤-2,
),m为常数且m≤-2,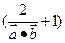 成立的
成立的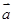 =(1,
=(1,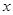 ),
),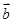 =(
=(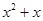 ,
,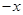 ),m为常数且m≤-2,
),m为常数且m≤-2,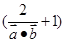 成立的
成立的