题目内容
如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC．M、N分别是AD、BE上点，将三角形ADE沿AE折起．下列说法正确的是______．（填上所有正确的序号）
①不论D折至何位置（不在平面ABC内）都有MN∥平面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置（不在平面ABC内）都有MN∥AB；
④在折起过程中，一定存在某个位置，使EC⊥AD．
①不论D折至何位置（不在平面ABC内）都有MN∥平面DEC；
②不论D折至何位置都有MN⊥AE；
③不论D折至何位置（不在平面ABC内）都有MN∥AB；
④在折起过程中，一定存在某个位置，使EC⊥AD．
由已知，在未折叠的原梯形中，AB∥DE，BE∥AD．所以四边形ABED为平行四边形，∴DA=EB．折叠后得出图形如下：
①过M，N分别作AE，BC的平行线，交ED，EC于F，H．连接FH
则
=
，
=
∵AM=BN，∴EN=DM，等量代换后得出HN=FM，
又CB∥EA，∴HN∥FM，
∴四边形MNHF是平行四边形．
∴MN∥FH
MN?面CED，HF?面CED．∴MN∥平面DEC． ①正确
②由已知，AE⊥ED，AE⊥EC，
∴AE⊥面CED，HF?面CED∴AE⊥HF，∴MN⊥AE；②正确
③MN与AB 异面．假若MN∥AB，则MN与AB确定平面MNAB，
从而BE?平面MNAB，AD?平面MNAB．与BE和AD是异面直线矛盾．③错误．
④当CE⊥ED时，EC⊥AD．
这是因为，由于CE⊥EA，EA∩ED=E，
所以CE⊥面AED，AD?面AED．得出EC⊥AD．④正确．
故答案为：①②④．
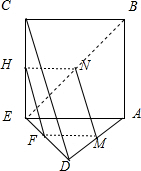
①过M，N分别作AE，BC的平行线，交ED，EC于F，H．连接FH
则
| HN |
| CB |
| EN |
| EB |
| FM |
| EA |
| DM |
| DA |
∵AM=BN，∴EN=DM，等量代换后得出HN=FM，
又CB∥EA，∴HN∥FM，
∴四边形MNHF是平行四边形．
∴MN∥FH
MN?面CED，HF?面CED．∴MN∥平面DEC． ①正确
②由已知，AE⊥ED，AE⊥EC，
∴AE⊥面CED，HF?面CED∴AE⊥HF，∴MN⊥AE；②正确
③MN与AB 异面．假若MN∥AB，则MN与AB确定平面MNAB，
从而BE?平面MNAB，AD?平面MNAB．与BE和AD是异面直线矛盾．③错误．
④当CE⊥ED时，EC⊥AD．
这是因为，由于CE⊥EA，EA∩ED=E，
所以CE⊥面AED，AD?面AED．得出EC⊥AD．④正确．
故答案为：①②④．
练习册系列答案
名题金卷系列答案
相关题目
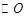的直径AB＝3，点C为
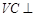平面ABC，且VC＝2，点M为线段VB的中点.
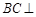平面VAC；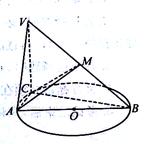
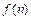对异面直线，则
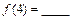；f(n)=______(答案用数字或n的解析式表示)