题目内容
【题目】如图，甲船从A处以每小时30海里的速度沿正北方向航行，乙船在B处沿固定方向匀速航行，B在A北偏西105°方向用与B相距10 
海里处．当甲船航行20分钟到达C处时，乙船航行到甲船的北偏西120°方向的D处，此时两船相距10海里． 
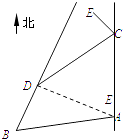
（1）求乙船每小时航行多少海里？
（2）在C的北偏西30°方向且与C相距 
海里处有一个暗礁E，周围 海里范围内为航行危险区域．问：甲、乙两船按原航向和速度航行有无危险？若有危险，则从有危险开始，经过多少小时后能脱离危险？若无危险，请说明理由．
【答案】
（1）解：如图，连接AD，CD，由题意CD=10，AC= 
=10，∠ACD=60°
∴△ACD是等边三角形，
∴AD=10，
∵∠DAB=45°
△ABD中，BD= 
=10，
∴v=10×3=30海里．
答：乙船每小时航行30海里．
（2）解：建立如图所示的坐标系，危险区域在以E为圆心，r= 
的圆内，直线BD的方程为y= 
x，∠DAB=∠DBA=45°
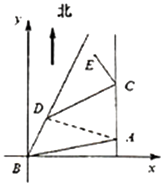
E的坐标为（ABcos15°﹣CEsin30°，ABsin15°+CEcos30°+AC），
求得A（5 +5，5 ﹣5），C（5 +5，5 +5），E（5+ 
，9+5 ），
E到直线BD的距离d1= 
=1＜ ，故乙船有危险；
点E到直线AC的距离d2= 
＞ ，故甲船没有危险．
以E为圆心，半径为 的圆截直线BD所得的弦长分别为l=2 
=2，
乙船遭遇危险持续时间为t= 
= 
（小时），
答：甲船没有危险，乙船有危险，且在遭遇危险持续时间 小时后能脱离危险．
【解析】（1）连接AD，CD，推断出△ACD是等边三角形，在△ABD中，利用余弦定理求得BD的值，进而求得乙船的速度．（2）建立如图所示的坐标系，危险区域在以E为圆心，r= 的圆内，求出E到直线BD的距离，与半径比较，即可得出结论．
