题目内容
13.过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程是x-3y+16=0.分析 求出直线$\frac{x}{2}$+$\frac{y}{6}$=1的斜率,从而得到过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程的斜率,由此能求出所求方程.
解答 解:∵直线$\frac{x}{2}$+$\frac{y}{6}$=1的斜率k=-3,
∴过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程的斜率k′=$\frac{1}{3}$,
∴过点(-1,5),且与直线$\frac{x}{2}$+$\frac{y}{6}$=1垂直的直线方程为:
$y-5=\frac{1}{3}(x+1)$,
整理,得x-3y+16=0.
故答案为:x-3y+16=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意直线与直线垂直的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.函数y=$\frac{2tanx}{1-tan^2x}$的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求: 如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线.
如图所示,已知D,E分别为△ABC的边AB,AC的中点,延长CD到M使DM=CD,延长BE至N使BE=EN.求证:M,A,N三点共线. 正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系.
正三棱柱ABC一A1B1C1的底面边长为2,D为AB上一点,如图,建立空间直角坐标系. 件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在
件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在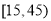 内的频数为92.
内的频数为92.
 的值;
的值; 内产品的个数;
内产品的个数;