题目内容
4.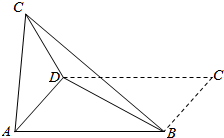 在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:
在平行四边形ABCD中,∠CBD=90°,BC=BD=1,将平行四边形沿对角线BD折成60°的二面角(如图中实线部分).求:(Ⅰ)A、C两点间的距离;
(Ⅱ)异面直线AC与BD所成的角.
分析 (Ⅰ)由$|\overrightarrow{AC}{|}^{2}$=|$\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{BC}$|2,∠CBD=90°,BC=BD=1,ABCD为平行四边形,从而|$\overrightarrow{AD}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{BC}$|=1,且$\overrightarrow{AD}⊥\overrightarrow{DB}$,$\overrightarrow{DB}⊥\overrightarrow{BC}$,<$\overrightarrow{AD},\overrightarrow{BC}$>=120°,由此能求出A、C两点间的距离.
(2)设<$\overrightarrow{AC},\overrightarrow{BD}$>=θ,则cosθ=$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}|•|\overrightarrow{BD}|}$=-$\frac{\overrightarrow{DC}•\overrightarrow{DB}}{\sqrt{2}}$,由∠CBD=90°,BC=BD=1,得<$\overrightarrow{DC},\overrightarrow{DB}$>=45°,由此能求出异面直线AC与BD所成的角.
解答 解:(Ⅰ)$|\overrightarrow{AC}{|}^{2}$=|$\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{BC}$|2
=|$\overrightarrow{AD}$|2+|$\overrightarrow{DB}$|2+|$\overrightarrow{BC}$|2+2$\overrightarrow{AD}•\overrightarrow{DB}$+2$\overrightarrow{AD}•\overrightarrow{BC}$+2$\overrightarrow{DB}•\overrightarrow{BC}$,
∵∠CBD=90°,BC=BD=1,ABCD为平行四边形,
∴|$\overrightarrow{AD}$|=|$\overrightarrow{DB}$|=|$\overrightarrow{BC}$|=1,且$\overrightarrow{AD}⊥\overrightarrow{DB}$,$\overrightarrow{DB}⊥\overrightarrow{BC}$,
∵二面角A-BD-C为60°,∴<$\overrightarrow{AD},\overrightarrow{BC}$>=120°,
∴$|\overrightarrow{AC}{|}^{2}$=|$\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{BC}$|2
=1+1+1+2×1×1×cos120°
=2,
∴|$\overrightarrow{AC}$|=$\sqrt{2}$.
∴A、C两点间的距离为$\sqrt{2}$.
(2)设<$\overrightarrow{AC},\overrightarrow{BD}$>=θ,
则cosθ=$\frac{\overrightarrow{AC}•\overrightarrow{BD}}{|\overrightarrow{AC}|•|\overrightarrow{BD}|}$=$\frac{(\overrightarrow{AD}+\overrightarrow{DC})•\overrightarrow{BD}}{\sqrt{2}}$
=$\frac{\overrightarrow{DC}•\overrightarrow{BD}}{\sqrt{2}}$=-$\frac{\overrightarrow{DC}•\overrightarrow{DB}}{\sqrt{2}}$,
在△CBD中,∠CBD=90°,BC=BD=1,
∴<$\overrightarrow{DC},\overrightarrow{DB}$>=45°,
∴cosθ=-$\frac{\overrightarrow{DC}•\overrightarrow{DB}}{\sqrt{2}}$=-$\frac{|\overrightarrow{DC}|•|\overrightarrow{DB}|•cos45°}{\sqrt{2}}$=-$\frac{\sqrt{2}}{2}$,
∴异面直线AC与BD所成的角为45°.
点评 本题考查两点间距离的求法,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

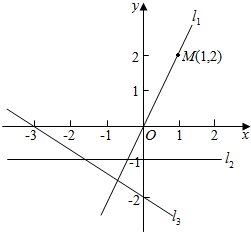 已知直线l1、l2、l3的位置如图所示,请写出直线l1、l2、l3的一般式方程.
已知直线l1、l2、l3的位置如图所示,请写出直线l1、l2、l3的一般式方程.