题目内容
3.用向量法证明:连接三角形两边中点的线段平行于第三边且等于第三边的一半.分析 可先作出图形△ABC,并设D,E分别为边AB,AC的中点,容易得到$\overrightarrow{DE}=\frac{1}{2}\overrightarrow{BC}$,从而便有DE∥BC,且$DE=\frac{1}{2}BC$,这样便得到结论:连接三角形两边中点的线段平行于第三边且等于第三边的一半.
解答 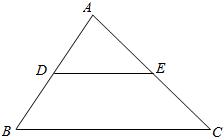 证明:如图,△ABC,D,E分别是AB,AC边的中点;
证明:如图,△ABC,D,E分别是AB,AC边的中点;
$\overrightarrow{DE}=\overrightarrow{AE}-\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}$=$\frac{1}{2}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{2}\overrightarrow{BC}$;
∴$\overrightarrow{DE}$∥$\overrightarrow{BC}$,且$|\overrightarrow{DE}|=\frac{1}{2}|\overrightarrow{BC}|$;
即DE∥BC,且DE=$\frac{1}{2}BC$;
∴连接三角形两边中点的线段平行于第三边且等于第三边的一半.
点评 考查向量法证明三角形中位线的性质,向量减法的几何意义,向量数乘的几何意义,以及向量的数乘运算.

练习册系列答案
相关题目
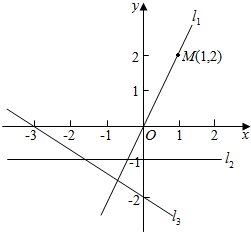 已知直线l1、l2、l3的位置如图所示,请写出直线l1、l2、l3的一般式方程.
已知直线l1、l2、l3的位置如图所示,请写出直线l1、l2、l3的一般式方程.