题目内容
已知矩阵A=
|
|
|
分析:根据特征值的定义可知Aα=λα,利用待定系数法建立四个等式关系,解四元一次方程组即可.
解答:解:由矩阵A属于特征值3的一个特征向量为α1=
可得
=3
,
即
;(4分)
由矩阵A属于特征值2的一个特征向量为α2=
,可得
=(-1)
,
即
,(6分)
解得
,即矩阵A=
.(10分)
|
|
|
|
即
|
由矩阵A属于特征值2的一个特征向量为α2=
|
|
|
|
即
|
解得
|
|
点评:本题主要考查了二阶矩阵,以及特征值与特征向量的计算,属于基础题.

练习册系列答案
相关题目
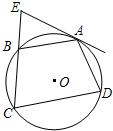 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.