题目内容
本题包括A、B两小题,考生都做.
A选修4-2:矩阵与变换
已知矩阵A=
,若矩阵A属于特征值3的一个特征向量为α1=
,属于特征值-1的一个特征向量为α2=
,求矩阵A.
B选修4-4:坐标系与参数方程
在直角坐标系x0y中,直线l的参数方程为
(t为参数),若以直角坐标系xOy的O点为极点,Ox为极轴,且长度单位相同,建立极坐标系,得曲线C的极坐标方程为ρ=2cos(θ-
).
(1)求直线l的倾斜角;
(2)若直线l与曲线l交于A、B两点,求AB.
A选修4-2:矩阵与变换
已知矩阵A=
|
|
|
B选修4-4:坐标系与参数方程
在直角坐标系x0y中,直线l的参数方程为
|
| π |
| 4 |
(1)求直线l的倾斜角;
(2)若直线l与曲线l交于A、B两点,求AB.
分析:A、利用矩阵特征值、特征向量的定义,建立方程组,即可求得矩阵A;
B、(1)利用参数方程可得
且θ∈[0,π),从而可得直线l的倾斜角;
(2)求出l的普通方程,ρ=2cos(θ-
)的直角坐标方程,求出圆心到直线l的距离,即可计算|AB|.
B、(1)利用参数方程可得
|
(2)求出l的普通方程,ρ=2cos(θ-
| π |
| 4 |
解答:A解:由矩阵A属于特征值3的一个特征向量为α1=
可得
=3
,
即
; …(4分)
由矩阵A属于特征值2的一个特征向量为α2=
,可得
=(-1)
,
即
…(6分)
解得
,即矩阵A=
…(10分)
B解:(1)设直线l的倾斜角为θ,则
且θ∈[0,π),∴θ=
,即直线l的倾斜角为
…(5分)
(2)l的普通方程为y=
x+
,ρ=2cos(θ-
)的直角坐标方程为(x-
)2+(y-
)2=1,
所以圆心(
,
)到直线l的距离d=
,
∴|AB|=
…(10分)
|
|
|
|
即
|
由矩阵A属于特征值2的一个特征向量为α2=
|
|
|
|
即
|
解得
|
|
B解:(1)设直线l的倾斜角为θ,则
|
| π |
| 3 |
| π |
| 3 |
(2)l的普通方程为y=
| 3 |
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
所以圆心(
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
∴|AB|=
| ||
| 2 |
点评:本题是选做题,考查矩阵与变换,考查坐标系与参数方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分, (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
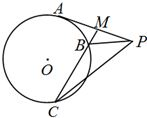
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.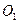 与圆
与圆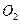 内切于点
内切于点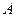 ,其半径分别为
,其半径分别为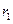 与
与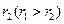 ,
,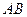 交圆
交圆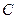 (
(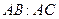 为定值。
为定值。