题目内容
已知平面向量
=(
,-1),
=(
,
).
(1)证明:|
+
|=|
-
|;
(2)若存在不同时为零的实数k和t,使
=
+(t2-3)
,
=-k
+t
,且
⊥
,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)-k=0的解的情况.
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
(1)证明:|
| a |
| b |
| a |
| b |
(2)若存在不同时为零的实数k和t,使
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
(3)据(2)的结论,讨论关于t的方程f(t)-k=0的解的情况.
分析:(1)利用向量的运算和模的计算公式即可得出;
(2)利用向量的数量积运算、垂直与数量积的关系即可得出;
(3)利用导数研究函数的单调性、极值即可得出.
(2)利用向量的数量积运算、垂直与数量积的关系即可得出;
(3)利用导数研究函数的单调性、极值即可得出.
解答:解:(1)∵
+
=(
+
,
-1),
-
=(
-
,-1-
).
∴|
+
|=
=
,|
-
|=
=
.
∴|
+
|=|
-
|;
(2)|
|=
=2,|
|=
=1,
•
=
×
-1×
=0.
∵
⊥
,∴
•
=[
+(t2-3)
]•(k
+t
)=k
2+t(t2-3)
2=2k+t(t2-3)=0.
∴k=-
t(t2-3).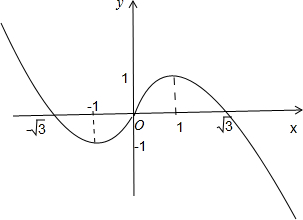
(3)由(2)可知:f(t)=-
t3+
t,
f′(t)=-
t2+
=-
(t+1)(t-1),令f′(x)=0,解得t=±1.
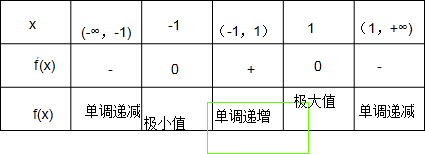
列表如下:
由表格可知:当x=-1时,函数f(x)取得极小值f(-1)=-1;
当x=1时,函数f(x)取得极大值f(1)=1.
因此:①当k=±1时,方程f(t)-k=0由两解;
②当-1<k<1时,方程f(t)-k=0由3个解;
③当k<-1或1<k时,方程f(t)-k=0由1个解.
| a |
| b |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| 3 |
| 1 |
| 2 |
| ||
| 2 |

∴|
| a |
| b |
(
|
| 5 |
| a |
| b |
(
|
| 5 |
∴|
| a |
| b |
| a |
| b |
(2)|
| a |
(
|
| b |
(
|
| a |
| b |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∵
| x |
| y |
| x |
| y |
| a |
| b |
| a |
| b |
| a |
| b |
∴k=-
| 1 |
| 2 |

(3)由(2)可知:f(t)=-
| 1 |
| 2 |
| 3 |
| 2 |
f′(t)=-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
列表如下:
由表格可知:当x=-1时,函数f(x)取得极小值f(-1)=-1;
当x=1时,函数f(x)取得极大值f(1)=1.
因此:①当k=±1时,方程f(t)-k=0由两解;
②当-1<k<1时,方程f(t)-k=0由3个解;
③当k<-1或1<k时,方程f(t)-k=0由1个解.
点评:熟练掌握向量的运算和模的计算公式、向量的数量积运算、垂直与数量积的关系、利用导数研究函数的单调性、极值等是解题的关键.

练习册系列答案
相关题目