题目内容
已知点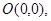
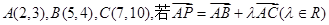
(1)是否存在 ,使得点P在第一、三象限的角平分线上?
,使得点P在第一、三象限的角平分线上?
(2)是否存在 ,使得四边形
,使得四边形 为平行四边形?(若存在,则求出
为平行四边形?(若存在,则求出 的值,若不存在,请说明理由.)
的值,若不存在,请说明理由.)
(1)存在;(2)不存在.
解析试题分析:(1)根据已知的等式求得P的坐标,再根据P在第一、三象限角平分线上可以得到P的坐标满足 ,从而可以建立关于
,从而可以建立关于 的方程,方程组的解的情况即是
的方程,方程组的解的情况即是 的存在情况;(2)由四边形OBPA是平行四边形,结合向量加法的平行四边形法则,可以得到
的存在情况;(2)由四边形OBPA是平行四边形,结合向量加法的平行四边形法则,可以得到 ,从而建立关于
,从而建立关于 的方程组,方程组的解的情况即是
的方程组,方程组的解的情况即是 的存在情况.
的存在情况.
(1)存在.
设 ,则
,则 ,∵
,∵ 3分
3分
由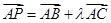 得
得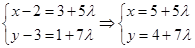 5分
5分
若点P在第一、三象限的角平分线上,则 ,即
,即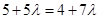 ,
, . 6分
. 6分
(2)不存在.
若四边形OBPA为平行四边形,则 8分
8分
∵ ,∴
,∴ ,方程组无解,因此满足条件的
,方程组无解,因此满足条件的 不存在 10分
不存在 10分
考点:1、向量的坐标运算;2、第一、三象限角平分线上点的坐标特点3、向量加法的平行四边形法则.

练习册系列答案
相关题目
 ,若
,若 ,则
,则 = .
= .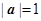 ,
,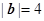 ,且向量
,且向量 与
与 不共线.
不共线. ,求
,求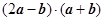 ;
; 与
与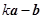 互相垂直,求
互相垂直,求 的值.
的值.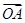 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).
=(5-m,-3-m). =2a-b,
=2a-b, =3a+b,
=3a+b,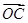 =a-3b,求证:A、B、C三点共线;
=a-3b,求证:A、B、C三点共线; ,-1),b=
,-1),b=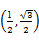 .
. 对应的复数为1+2i,向量
对应的复数为1+2i,向量 对应的复数为3-i.
对应的复数为3-i. ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线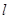 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 =sin2θ·
=sin2θ· +cos2θ·
+cos2θ· (θ∈R),则(
(θ∈R),则( +
+ )·
)· 的最小值是________.
的最小值是________.