题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{3}+{x}^{2},x<1}\\{alnx,x≥1}\end{array}\right.$,a∈R.(1)当x<1时,求函数f(x)的单调区间和极值;
(2)对任意给定的正实数a,曲线y=f(x)上是否存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?
分析 (1)当x<1时,f(x)=-x3+x2,求导f′(x)=-3x2+2x=-3x(x-$\frac{2}{3}$),从而由导数的正负确定函数的单调性及极值;
(2)假设曲线y=f(x)上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,由题意可设P(t,f(t))(t>0),则Q(-t,t3+t2),且t≠1,由$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0可得-t2+f(t)(t3+t2)=0,从而讨论判断方程是否有解即可.
解答 解:(1)当x<1时,f(x)=-x3+x2,
f′(x)=-3x2+2x=-3x(x-$\frac{2}{3}$),
故f(x)在(-∞,0)和($\frac{2}{3}$,1)上单调递减,在(0,$\frac{2}{3}$)上单调递增.
∴当x=0时,f(x)取得极小值f(0)=0;
当x=$\frac{2}{3}$时,f(x)取得极大值f($\frac{2}{3}$)=$\frac{4}{27}$.
(2)假设曲线y=f(x)上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,
则P,Q只能在y轴的两侧,不妨设P(t,f(t))(t>0),则Q(-t,t3+t2),且t≠1.
因为△POQ是以O为直角顶点的直角三角形,
所以$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,
即:-t2+f(t)(t3+t2)=0 ①,
是否存在点P,Q等价于方程①是否有解.
若0<t<1,则f(t)=-t3+t2,
代入方程①得:t4-t2+1=0,此方程无实数解;
若t≥1,则f(t)=alnt,代入方程①得:$\frac{1}{a}$=(t+1)lnt,
设h(t)=(t+1)lnt(t≥1),
则h′(t)=lnt+$\frac{1}{t}$+1>0在[1,+∞)上恒成立,
所以h(t)在[1,+∞)上单调递增,
从而h(t)≥h(1)=0,
所以当a>0时,方程$\frac{1}{a}$=(t+1)lnt有解.
所以,对任意给定的正实数a,曲线y=f(x)上存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上.
点评 本题考查了导数的综合应用及平面向量的应用,同时考查了分类讨论的思想应用.

| A. | $\frac{5}{18}$ | B. | -$\frac{5}{18}$ | C. | $\frac{7}{9}$ | D. | -$\frac{7}{9}$ |
 函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )
函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )| A. | 2011 | B. | $\frac{4023}{2}$ | C. | 2012 | D. | $\frac{4025}{2}$ |
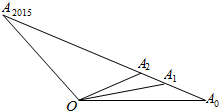 如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).
如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).