题目内容
13.在等比数列{an}中,a1=$\frac{1}{4}$,8a2,3a3,a4成等差数列.(1)求数列{an}的通项公式;
(2)令bn=log16an,求数列{bn}的前n项和Sn.
分析 (1)由等比数列通项公式和等差数列的性质,列出方程,求出公比,由此能求出数列{an}的通项公式.
(2)当an=2×$(\frac{1}{4})^{n-1}$时,bn=log16an=$\frac{3}{4}-\frac{n}{2}$,当${a}_{n}=(\frac{1}{4})^{n-2}$时,bn=log16an=1-$\frac{n}{2}$,由此利用分组求和法能求出数列{bn}的前n项和.
解答 解:(1)∵在等比数列{an}中,a1=$\frac{1}{4}$,8a2,3a3,a4成等差数列,
∴2[3×($\frac{1}{4}{q}^{2}$)]=$8×(\frac{1}{4}q)$+$\frac{1}{4}{q}^{3}$,
解得q=2或q=4或q=0(舍),
∴${a}_{n}=2×(\frac{1}{4})^{n-1}$或${a}_{n}=4×(\frac{1}{4})^{n-1}$=($\frac{1}{4}$)n-2.
(2)当an=2×$(\frac{1}{4})^{n-1}$时,bn=log16an=$lo{g}_{16}[2×(\frac{1}{4})^{n-1}]$=$lo{g}_{16}{2}^{3-2n}$=$\frac{3-2n}{4}$=$\frac{3}{4}-\frac{n}{2}$,
∴数列{bn}的前n项和:
Sn=$\frac{3}{4}n-\frac{1}{2}(1+2+3+…+n)$=$\frac{3}{4}n-\frac{1}{2}×\frac{n(n+1)}{2}$=$\frac{n}{2}-\frac{{n}^{2}}{4}$;
当${a}_{n}=(\frac{1}{4})^{n-2}$时,bn=log16an=log16[($\frac{1}{4}$)n-2]=1-$\frac{n}{2}$,
∴数列{bn}的前n项和:
Sn=n-$\frac{1}{2}(1+2+3+…+n)$=n-$\frac{1}{2}×\frac{n(n+1)}{2}$=$\frac{3n}{4}-\frac{{n}^{2}}{4}$.
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意等差数列、等比数列的性质和分组求和法的合理运用.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
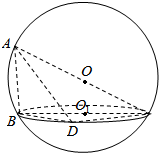 如图所示,AC为球O的直径,BC是截面圆O1的直径,点D在圆O1上,根据球的截面性质:球心和截面圆心的连线垂直于截面,求证:
如图所示,AC为球O的直径,BC是截面圆O1的直径,点D在圆O1上,根据球的截面性质:球心和截面圆心的连线垂直于截面,求证: