题目内容
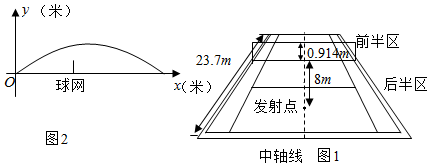
18. 函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )
函数f(x)=Asin(ωx+φ)+b的图象如图所示,则f(1)+f(2)+…+f(2012)=( )| A. | 2011 | B. | $\frac{4023}{2}$ | C. | 2012 | D. | $\frac{4025}{2}$ |
分析 由函数y=Asin(ωx+φ)的部分图象求出解析式,再利用函数的周期性求得所求式子的值.
解答 解:由函数f(x)=Asin(ωx+φ)+b的图象可得 b=1;A=1.5-1=0.5;$\frac{2π}{ω}$=4,ω=$\frac{π}{2}$;φ=0.
故函数f(x)=0.5sin($\frac{π}{2}$x)+1,
故f(1)+f(2)+f(3)+f(4)=1.5+1+0.5+1=4,
故f(1)+f(2)+…+f(2012)=503×4=2012,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,利用函数的周期性求函数的值,属于中档题.

练习册系列答案
相关题目
6.已知命题甲为:x>0;命题乙为x2>0,那么( )
| A. | 甲是乙的充要条件 | B. | 甲是乙的充分非必要条件 | ||
| C. | 甲是乙的必要不充分条件 | D. | 甲是乙的既不充分也不必要条件 |
8.若$\overrightarrow{OA}$=3e1,$\overrightarrow{OB}$=7e2,$\overrightarrow{PB}$=4$\overrightarrow{AP}$,$\overrightarrow{OP}$=me1+ne2,则m-n等于( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |