题目内容
20.已知二次函数f(x)满足f(x+1)-f(x)=2x,且0是函数y=f(x)-1的一个零点.(1)求f(x)的解析式;
(2)当x∈[-2,1]时,不等式f(x)>2x+m恒成立,求实数m的取值范围.
分析 (1)设出f(x)=ax2+bx+c(a≠0),由f(0)=1和f(x+1)-f(x)=2x,得到系数的关系,解得a,b,c,进而得到解析式;
(2)由题意可得x2-3x+1>m,恒成立,令g(x)=x2-3x+1 x∈[-2,1],由单调性求得最小值即可.
解答 解:(1)因为f(x)是二次函数,
所以设f(x)=ax2+bx+c(a≠0),
因为0是y=f(x)-1的一个零点,
所以f(0)-1=0,所以c=1,
又因为f(x+1)-f(x)=2x,
即a(x+1)2+b(x+1)+c-ax2-bx-c=2x,
所以2(a-1)x+(a+b)=0,
所以2(a-1)=a+b=0,所以a=1,b=-1
所以f(x)=x2-x+1;
(2)不等式x2-x+1>2x+m可化为x2-3x+1>m,
令g(x)=x2-3x+1 x∈[-2,1],
因为g(x)的对称轴为$x=\frac{3}{2}$,
所以g(x)在[-2,1]上是单调递减的,
所以g(x)min=g(1)=-1,
所以m<-1.
点评 本题考查二次函数的解析式的求法,注意运用待定系数法,同时考查二次不等式恒成立问题,注意转化为求二次函数在闭区间的最值问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.若直线a⊥平面α,平面β⊥平面α,则a与β的位置关系为( )
| A. | a与β相交 | B. | a∥β | C. | a?β | D. | a∥β或a?β |
8.曲线y=1+$\sqrt{4-{x}^{2}}$与直线y=k(x+2)+5有两个交点,则实数k的取值范围是( )
| A. | [-1,-$\frac{3}{4}$) | B. | (-∞,-1] | C. | (-$\frac{3}{4}$,0] | D. | [-1,0] |
12.阅读如图的程序框图,运行相应的程序,若输入x的值为2,则输出y的值为( )
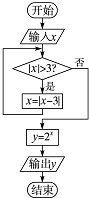

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
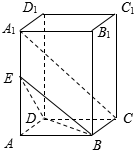 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,E为A1A的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,E为A1A的中点.