题目内容
20.如图所示,AM是△ABC的BC边上的中线,试说明:AB2+AC2=2(AM2+BM2).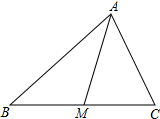
分析 利用勾股定理得AB2+AC2=2AM2-2DM2+BD2+CD2,进而由BD2=MC2+2MC•DM+DM2,CD2=MC2-2MC•DM+DM2,求出即可.
解答  证明:如图,作BC边上的高AD交BC于D,
证明:如图,作BC边上的高AD交BC于D,
则在Rt△ABD中,AB2=BD2+AD2,
在Rt△ACD中,AC2=CD2+AD2,
所以AB2+AC2=2AD2+BD2+CD2,
在在Rt△ADM中,AD2=AM2-DM2,
则AB2+AC2=2AM2-2DM2+BD2+CD2,
∵AM是△ABC的BC边上的中线,
∴BM=MC,
∴BD2=(BM+DM)2=(MC+DM)2=MC2+2MC•DM+DM2,
CD2=(MC-DM)2=MC2-2MC•DM+DM2,
∴AB2+AC2=2AM2-2DM2+MC2+2MC•DM+DM2+MC2-2MC•DM+DM2,
∴AB2+AC2=2(AM2+BM2).
点评 本题考查勾股定理,三角形的中线及高的定义以及完全平方公式,需熟练掌握,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.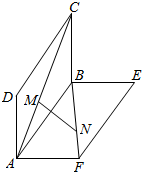 如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )
如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )
 如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )
如图所示,四边形ABCD、ABEF都是矩形,它们所在的平面互相垂直,AD=AF=1,AB=2,点M、N分别在它们的对角线AC、BF上,且CM=BN=a(0<a<$\sqrt{5}$),当MN的长最小时,a的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{5}}{4}$ | D. | $\frac{\sqrt{10}}{3}$ |
10. 如图,直二面角α-l-β中,AB?α,CD?β,AB⊥l,CD⊥l,垂足分别为B、C,且AB=BC=CD=1,则AD的长等于( )
如图,直二面角α-l-β中,AB?α,CD?β,AB⊥l,CD⊥l,垂足分别为B、C,且AB=BC=CD=1,则AD的长等于( )
 如图,直二面角α-l-β中,AB?α,CD?β,AB⊥l,CD⊥l,垂足分别为B、C,且AB=BC=CD=1,则AD的长等于( )
如图,直二面角α-l-β中,AB?α,CD?β,AB⊥l,CD⊥l,垂足分别为B、C,且AB=BC=CD=1,则AD的长等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
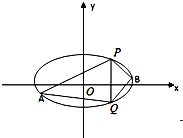 已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点.
已知椭圆C的中心在原点,焦点在X轴上,离心率等于$\frac{1}{2}$,它的两个顶点恰好是双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{3}$=1的焦点. 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BCA=45°,AP=AD=AC=2.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BCA=45°,AP=AD=AC=2.