题目内容
【题目】已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点与抛物线y2=4x的焦点F重合.
,右焦点与抛物线y2=4x的焦点F重合.
(1)求椭圆的方程;
(2)过F的直线l交椭圆于A、B两点,椭圆的左焦点力F',求△AF'B的面积的最大值.
【答案】
(1)解:根据题意,得F(1,0),∴c=1,
又 ![]() ,∴a=2,∴b2=a2﹣c2=3,
,∴a=2,∴b2=a2﹣c2=3,
∴椭圆的方程为: ![]()
(2)解:显然l的斜率不为0,设l:x=my+1,
联立直线l与椭圆方程 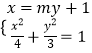 ,化简,得(3m2+4)y2+6my﹣9=0,
,化简,得(3m2+4)y2+6my﹣9=0,
设A(x1,y1),B(x2,y2),则△>0恒成立,
由韦达定理,得y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,
,
∴ ![]() =
= ![]()
=|y1﹣y2|
= ![]()
= ![]()
= ![]() ,
,
令t= ![]() ,t≥1,则m2=t2﹣1,
,t≥1,则m2=t2﹣1,
∴ ![]() =
= ![]() =
= ![]() ,
,
令 ![]() (t≥1),则
(t≥1),则 ![]() =
= ![]() >0,
>0,
∴u(t)在[1,+∞)上单调递增,
∴当t=1即m=0时,umin(t)=u(1)=4,( ![]() )max=3,
)max=3,
故当m=0时,△AF'B的面积的最大值为3
【解析】(1)根据题意得F(1,0),即c=1,再通过 ![]() 及c2=a2﹣b2计算可得椭圆的方程;(2)由题设l:x=my+1,A(x1 , y1),B(x2 , y2),联立直线l与椭圆方程,结合韦达定理,得
及c2=a2﹣b2计算可得椭圆的方程;(2)由题设l:x=my+1,A(x1 , y1),B(x2 , y2),联立直线l与椭圆方程,结合韦达定理,得 ![]() =
= ![]() ,利用换元法计算即可.
,利用换元法计算即可.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目