题目内容
9.已知动点P与两定点A(-2,0),B(2,0)连线的斜率之积为-$\frac{1}{4}$.(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)若过点F(-$\sqrt{3}$,0)的直线l与轨迹C交于M、N两点,且轨迹C上存在点E使得四边形OMEN(O为坐标原点)为平行四边形,求直线l的方程.
分析 (Ⅰ)设出P的坐标,由${k}_{PA}•{k}_{PB}=-\frac{1}{4}$化简整理可得曲线C的方程;
(Ⅱ)设M(x1,y1),N(x2,y2),由题意知l的斜率一定不为0,设l:x=my-$\sqrt{3}$,代入椭圆方程整理得(m2+4)y2-$2\sqrt{3}$my-1=0,假设存在点E,使得四边形OMEN为平行四边形,其充要条件为$\overrightarrow{OE}=\overrightarrow{OM}+\overrightarrow{ON}$,则点E的坐标为(x1+x2,y1+y2).由此利用韦达定理结合已知条件能求出直线l的方程.
解答 解:(Ⅰ)设P(x,y),由${k}_{PA}•{k}_{PB}=-\frac{1}{4}$,得
$\frac{y}{x+2}•\frac{y}{x-2}=-\frac{1}{4}$,整理得:$\frac{{x}^{2}}{4}+{y}^{2}=1$.
∴曲线C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)设M(x1,y1),N(x2,y2),由题意知l的斜率一定不为0,
故不妨设l:x=my-$\sqrt{3}$,代入椭圆方程整理得(m2+4)y2-$2\sqrt{3}$my-1=0,
△=12m2+4m2+16=16m2+16>0,
则${y}_{1}+{y}_{2}=\frac{2\sqrt{3}m}{{m}^{2}+4},{y}_{1}{y}_{2}=-\frac{1}{{m}^{2}+4}$,①
假设存在点E,使得四边形OMEN为平行四边形,
其充要条件为$\overrightarrow{OE}=\overrightarrow{OM}+\overrightarrow{ON}$,则点E的坐标为(x1+x2,y1+y2).
由点E在椭圆上,即$\frac{({x}_{1}+{x}_{2})^{2}}{4}+({y}_{1}+{y}_{2})^{2}=1$,
整理得${{x}_{1}}^{2}+{{x}_{2}}^{2}+4{{y}_{1}}^{2}+4{{y}_{2}}^{2}+2{x}_{1}{x}_{2}+8{y}_{1}{y}_{2}-4=0$.
又M,N在椭圆上,即${{x}_{1}}^{2}+4{{y}_{1}}^{2}=4,{{x}_{2}}^{2}+4{{y}_{2}}^{2}=4$,
故x1x2+4y1y2=-2,②
又${x}_{1}{x}_{2}=(m{y}_{1}-\sqrt{3})(m{y}_{2}-\sqrt{3})$=${m}^{2}{y}_{1}{y}_{2}-\sqrt{3}m({y}_{1}+{y}_{2})+3$,
将①②代入上式解得m=±$\frac{2\sqrt{5}}{5}$
即直线l的方程是:x=±$\frac{2\sqrt{5}}{5}$y+1,
即$\sqrt{5}x±2y-\sqrt{5}=0$.
点评 本题考查点的轨迹方程的求法,考查满足条件的点是否存在的判断与直线方程的求法,体现了数学转化思想方法,注意函数与方程思想的合理运用,是中档题.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案| A. | 1.55 | B. | 1.65 | C. | 1.75 | D. | 1.85 |
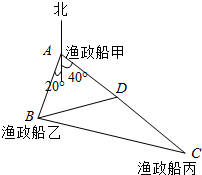 2015年6号台风“红霞”5月12日上午8点在日本本州和歌由县西南东海东部海面登陆,某渔船丙由于发动机故障急需救援,如图,正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲140km的C处,渔政船乙在渔政船甲的南偏东西20°方向的B处,两艘渔政船协调后立即让渔政船甲向渔船丙所在位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行60km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿着直线BC航行前去救援渔船丙),此时B、D两处相距84km,问渔政船乙要航行多少距离才能到达渔船所在的位置C处实施营救.
2015年6号台风“红霞”5月12日上午8点在日本本州和歌由县西南东海东部海面登陆,某渔船丙由于发动机故障急需救援,如图,正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙,同时收到同一片海域上渔船丙的求救信号,此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲140km的C处,渔政船乙在渔政船甲的南偏东西20°方向的B处,两艘渔政船协调后立即让渔政船甲向渔船丙所在位置C处沿直线AC航行前去救援,渔政船乙仍留在B处执行任务,渔政船甲航行60km到达D处时,收到新的指令另有重要任务必须执行,于是立即通知在B处执行任务的渔政船乙前去救援渔船丙(渔政船乙沿着直线BC航行前去救援渔船丙),此时B、D两处相距84km,问渔政船乙要航行多少距离才能到达渔船所在的位置C处实施营救.