题目内容
一个棱长为1的正方体,则该正方体的正视图的面积不可能等于
A.1 B.
C.
D.
.
A.1 B.
| 2 |
| ||
| 2 |
| ||
| 2 |
分析:根据正方体的正视图的边长变化,求出正视图的面积的取值范围即可判断.
解答:解:∵正方体的棱长为1,
∴正方形的对角线长为
,
∴当正方形的边长作为正视图的底面边长上,此时面积的最小值为S=1×1=1,
当正方形的对角线作为正视图的底面边长上,此时面积的最大值为S=1×
=
,
∴正方体的正视图的面积S的取值范围是[1,
].
∵
∉[1,
],
∴C不成立,
故答案为:C.
∴正方形的对角线长为
| 2 |
∴当正方形的边长作为正视图的底面边长上,此时面积的最小值为S=1×1=1,
当正方形的对角线作为正视图的底面边长上,此时面积的最大值为S=1×
| 2 |
| 2 |
∴正方体的正视图的面积S的取值范围是[1,
| 2 |
∵
| ||
| 2 |
| 2 |
∴C不成立,
故答案为:C.
点评:本题主要考查空间几何体中正视图的取值范围,根据不同的视角,得到正视图对应矩形的面积的最大值和最小值是解决本题的关键,利用函数的角度研究面积的取值范围是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
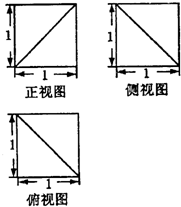 从一个棱长为1的正方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为
从一个棱长为1的正方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为 一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若要拼成一个棱长为1的正方体,则需要这样的几何体
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若要拼成一个棱长为1的正方体,则需要这样的几何体 (2012•咸阳三模)从一个棱长为1的正方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为( )
(2012•咸阳三模)从一个棱长为1的正方体中切去一部分,得到一个几何体,其三视图如图,则该几何体的体积为( )