题目内容
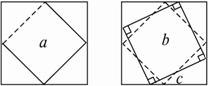
有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
分析:首先想象一下,当正方体绕着对角线BD'所在的直线转动时,体会投影的变化,当正方体为ABCD-A'B'C'D'投影最大的时候,应该是投影面α和面AB'C平行,从而得到结果.
解答: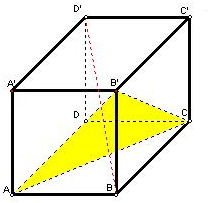 解:设正方体为ABCD-A'B'C'D'投影最大的时候,是投影面α和面AB'C平行,
解:设正方体为ABCD-A'B'C'D'投影最大的时候,是投影面α和面AB'C平行,
三个面的投影为三个全等的菱形,其对角线为
,即投影上三条对角线构成边长为
的等边三角形.
∴投影的面积=2S△AB′C=
×
×
×2=
.
故选D.
 解:设正方体为ABCD-A'B'C'D'投影最大的时候,是投影面α和面AB'C平行,
解:设正方体为ABCD-A'B'C'D'投影最大的时候,是投影面α和面AB'C平行,三个面的投影为三个全等的菱形,其对角线为
| 2 |
| 2 |
∴投影的面积=2S△AB′C=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 3 |
故选D.
点评:本题考查平行投影及平行投影作图法,本题是一个计算投影面积的题目,注意解题过程中的投影图的变化情况,本题是一个中档题

练习册系列答案
相关题目
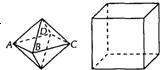
 9、两相同的正四棱锥组成左图所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )
9、两相同的正四棱锥组成左图所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有( )